《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

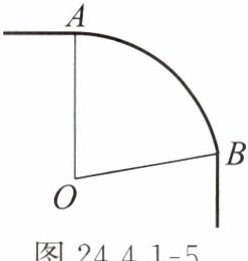
1. (甘肃中考)如图 24.4.1 - 5,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧($\overset{\frown}{AB}$),点 O 是这段弧所在圆的圆心,半径 OA = 90 m,圆心角∠AOB = 80°,则这段弯路($\overset{\frown}{AB}$)的长度为(C)

A.20π m
B.30π m
C.40π m
D.50π m

答案： C

2. 一定滑轮的起重装置如图 24.4.1 - 6,滑轮半径为 12 cm,当重物上升 4π cm 时,滑轮的一条半径 OA 按逆时针方向旋图 24.4.1 - 6 转的度数为(假设绳索与滑轮之间没有滑动)(C)

A.12°
B.30°
C.60°
D.90°

答案： C

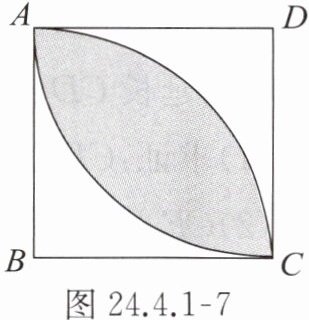
3. 如图 24.4.1 - 7,在正方形 ABCD 中,分别以 B,D 为圆心,以正方形的边长 a 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为(A)

A.πa
B.2πa
C.$\frac{1}{2}$πa
D.3a

答案： A

4. 已知扇形的面积为 2π,半径为 3,则该扇形的弧长为$\frac{4\pi}{3}$（结果保留 π）.

答案： $\frac{4\pi}{3}$（或写为“$\frac{4}{3}\pi$”）

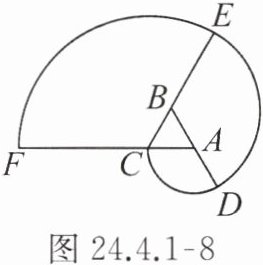
5. 如图 24.4.1 - 8,△ABC 是等边三角形,曲线 CDEF 是该三角形的“渐开线”,其中$\overset{\frown}{CD}$,$\overset{\frown}{DE}$,$\overset{\frown}{EF}$的圆心依次是 A,B,C,如果 AB = 1,那么曲线 CDEF 的长是4π.
 

答案： 4π

6. 如图 24.4.1 - 9,小方格都是边长为 1 的正方形,则以格点为圆心,以 1 或 2 为半径的两种弧围成的“叶状”阴影图案的面积为$2π - 4$.

答案： 连接叶状图案的两个端点，形成一个边长为2的正方形。以正方形的两个相邻顶点为圆心，2为半径作两个四分之一圆，每个四分之一圆的面积为$\frac{1}{4}π×2² = π$，两个四分之一圆的面积和为$2π$。正方形的面积为$2×2 = 4$。叶状阴影图案的面积为两个四分之一圆的面积和减去正方形的面积，即$2π - 4$。
$2π - 4$

7. 如图 24.4.1 - 10,已知 CB 是⊙O 的弦,CD 是⊙O 的直径,点 A 为 CD 延长线上一点,且 BC = AB,∠A = 30°.
(1) 求证：AB 是⊙O 的切线；
(2) 若⊙O 的半径为 2,求$\overset{\frown}{BD}$的长.

答案：
(1) 连接 $ OB $。
∵ $ OB = OC $，
∴ $ \angle OBC = \angle OCB $。
∵ $ AB = BC $，
∴ $ \angle A = \angle OCB $。
∵ $ \angle A = 30° $，
∴ $ \angle OCB = 30° $，$ \angle OBC = 30° $。
在 $ \triangle ABC $ 中，$ \angle ABC = 180° - \angle A - \angle OCB = 120° $。
∴ $ \angle ABO = \angle ABC - \angle OBC = 120° - 30° = 90° $，即 $ OB \perp AB $。
∵ $ OB $ 是 $ \odot O $ 的半径，
∴ $ AB $ 是 $ \odot O $ 的切线。
(2)
∵ $ \angle OBC = \angle OCB = 30° $，
∴ $ \angle BOC = 180° - 30° - 30° = 120° $。
∵ $ CD $ 是直径，
∴ $ \angle COD = 180° $，
∴ $ \angle BOD = \angle COD - \angle BOC = 180° - 120° = 60° $。
∵ $ \odot O $ 半径 $ r = 2 $，
∴ $ \overset{\frown}{BD} $ 的长为 $ \frac{60\pi × 2}{180} = \frac{2\pi}{3} $。