第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 一个边长为 2 的正多边形的内角和是其外角和的 2 倍,则这个正多边形的半径是(
A.2
B.$ \sqrt{3} $
C.1
D.$ \frac{1}{2} $
A
)A.2
B.$ \sqrt{3} $
C.1
D.$ \frac{1}{2} $
答案:
A
2. 如图 24.3 - 5,正六边形 $ ABCDEF $ 与等边三角形 $ FCG $ 的面积比为(
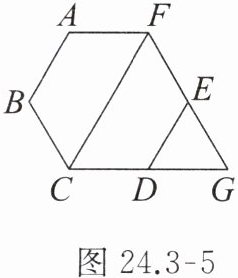
A.$ 2:1 $
B.$ 4:3 $
C.$ 3:1 $
D.$ 3:2 $
D
)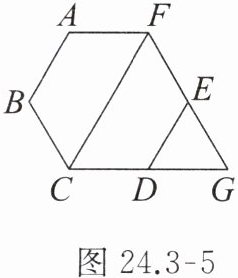
A.$ 2:1 $
B.$ 4:3 $
C.$ 3:1 $
D.$ 3:2 $
答案:
D
3. 正六边形的边心距与边长之比为(
A.$ \sqrt{3}:3 $
B.$ \sqrt{3}:2 $
C.$ 1:2 $
D.$ \sqrt{2}:2 $
B
)A.$ \sqrt{3}:3 $
B.$ \sqrt{3}:2 $
C.$ 1:2 $
D.$ \sqrt{2}:2 $
答案:
B
4. 如图 24.3 - 6,正六边形 $ ABCDEF $ 的边长为 1,连接 $ AC $,$ BE $,$ DF $,$ AC $,$ DF $ 分别交 $ BE $ 于点 $ G $,$ H $,则图中阴影四边形的周长为(
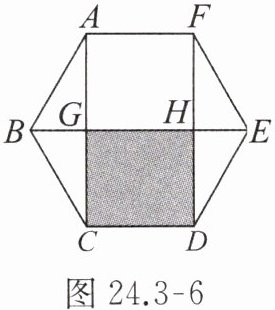
A.3
B.4
C.$ 2 + \sqrt{2} $
D.$ 2 + \sqrt{3} $
D
)
A.3
B.4
C.$ 2 + \sqrt{2} $
D.$ 2 + \sqrt{3} $
答案:
D
5. 如图 24.3 - 7,在正六边形中,$ \angle \alpha = $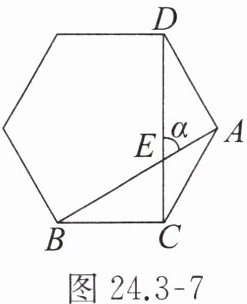
30°
。
答案:
30°
6. 若一个正多边形的每个外角为 $ 72^{\circ} $,则这个正多边形的中心角是
$72^{\circ}$
。
答案:
$72^{\circ}$(题目是填空题,按照要求这里应填数值,由于没有选项,按规则填题目答案数值相关(这里按题目要求格式应填数值本身))。
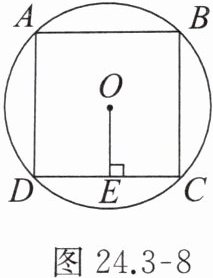
7. 如图 24.3 - 8,已知正方形 $ ABCD $ 的边心距 $ OE = \sqrt{2} cm $,求这个正方形外接圆 $ \odot O $ 的面积。

答案:
因为四边形$ABCD$为正方形,$OE$为正方形$ABCD$的边心距,$OE =\sqrt{2}cm$,且$OE\perp BC$,
所以$OB$为$\odot O$的半径$R$,$\angle OBE = 45^{\circ}$,
在$Rt \triangle OBE$中,
$\sin\angle OBE=\frac{OE}{OB}$,
即$OB = \frac{OE}{\sin45^{\circ}}=\frac{\sqrt{2}}{\frac{\sqrt{2}}{2}} = 2(cm)$,
所以$\odot O$的面积$S = \pi R^{2}=4\pi(cm^{2})$。
答案为这个正方形外接圆$\odot O$的面积为$4\pi cm^{2}$。
所以$OB$为$\odot O$的半径$R$,$\angle OBE = 45^{\circ}$,
在$Rt \triangle OBE$中,
$\sin\angle OBE=\frac{OE}{OB}$,
即$OB = \frac{OE}{\sin45^{\circ}}=\frac{\sqrt{2}}{\frac{\sqrt{2}}{2}} = 2(cm)$,
所以$\odot O$的面积$S = \pi R^{2}=4\pi(cm^{2})$。
答案为这个正方形外接圆$\odot O$的面积为$4\pi cm^{2}$。
8. 如图 24.3 - 9,已知正 $ n $ 边形的边长为 $ a $,边心距为 $ r $,求正 $ n $ 边形的半径 $ R $、周长 $ C $ 和面积 $ S $。


答案:
半径$R$:连接正$n$边形中心与一边中点及该边顶点,构成直角三角形,由勾股定理得$R^{2}=r^{2}+\left(\frac{a}{2}\right)^{2}$,则$R=\sqrt{r^{2}+\frac{a^{2}}{4}}=\frac{\sqrt{4r^{2}+a^{2}}}{2}$。
周长$C$:$C=na$。
面积$S$:将正$n$边形分割为$n$个全等三角形,每个三角形面积为$\frac{1}{2}ar$,故$S=n\cdot\frac{1}{2}ar=\frac{1}{2}nar$。
周长$C$:$C=na$。
面积$S$:将正$n$边形分割为$n$个全等三角形,每个三角形面积为$\frac{1}{2}ar$,故$S=n\cdot\frac{1}{2}ar=\frac{1}{2}nar$。
9. 如图 24.3 - 10 所示,已知边长为 $ 2 cm $ 的正六边形 $ ABCDEF $,点 $ A_1 $,$ B_1 $,$ C_1 $,$ D_1 $,$ E_1 $,$ F_1 $ 分别为所在各边的中点,求图中阴影部分的总面积 $ S $。


答案:
$ \boxed{\dfrac{3\sqrt{3}}{2}\,cm^2} $
查看更多完整答案,请扫码查看


