第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
一、正多边形的有关证明
【例 1】如图 24.3 - 1,五边形 $ ABCDE $ 内接于 $ \odot O $,$ \angle A = \angle B = \angle C = \angle D = \angle E $。求证:五边形 $ ABCDE $ 是正五边形。
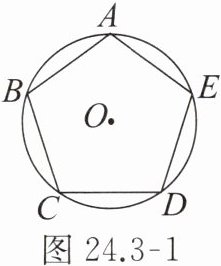
证明:
【例 1】如图 24.3 - 1,五边形 $ ABCDE $ 内接于 $ \odot O $,$ \angle A = \angle B = \angle C = \angle D = \angle E $。求证:五边形 $ ABCDE $ 是正五边形。
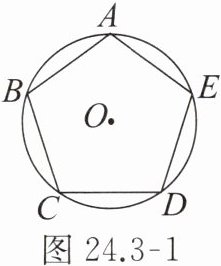
证明:
答案:
∵五边形$ABCDE$内接于$\odot O$,设弧$AB=\alpha$,弧$BC=\beta$,弧$CD=\gamma$,弧$DE=\delta$,弧$EA=\varepsilon$,则$\alpha+\beta+\gamma+\delta+\varepsilon=360°$。
$\angle A$是圆周角,所对优弧为弧$BCD$,其度数为$360°-(\varepsilon+\alpha)$,故$\angle A=\frac{1}{2}(360°-(\varepsilon+\alpha))$。
同理,$\angle B=\frac{1}{2}(360°-(\alpha+\beta))$,$\angle C=\frac{1}{2}(360°-(\beta+\gamma))$,$\angle D=\frac{1}{2}(360°-(\gamma+\delta))$,$\angle E=\frac{1}{2}(360°-(\delta+\varepsilon))$。
$\because\angle A=\angle B=\angle C=\angle D=\angle E$,
$\therefore\frac{1}{2}(360°-(\varepsilon+\alpha))=\frac{1}{2}(360°-(\alpha+\beta))\Rightarrow\varepsilon=\beta$;
同理可得$\alpha=\gamma$,$\beta=\delta$,$\gamma=\varepsilon$,
$\therefore\alpha=\beta=\gamma=\delta=\varepsilon$,即各弧相等。
$\because$同圆中相等弧所对弦相等,$\therefore AB=BC=CD=DE=EA$。
又$\angle A=\angle B=\angle C=\angle D=\angle E$,
$\therefore$五边形$ABCDE$是正五边形。
∵五边形$ABCDE$内接于$\odot O$,设弧$AB=\alpha$,弧$BC=\beta$,弧$CD=\gamma$,弧$DE=\delta$,弧$EA=\varepsilon$,则$\alpha+\beta+\gamma+\delta+\varepsilon=360°$。
$\angle A$是圆周角,所对优弧为弧$BCD$,其度数为$360°-(\varepsilon+\alpha)$,故$\angle A=\frac{1}{2}(360°-(\varepsilon+\alpha))$。
同理,$\angle B=\frac{1}{2}(360°-(\alpha+\beta))$,$\angle C=\frac{1}{2}(360°-(\beta+\gamma))$,$\angle D=\frac{1}{2}(360°-(\gamma+\delta))$,$\angle E=\frac{1}{2}(360°-(\delta+\varepsilon))$。
$\because\angle A=\angle B=\angle C=\angle D=\angle E$,
$\therefore\frac{1}{2}(360°-(\varepsilon+\alpha))=\frac{1}{2}(360°-(\alpha+\beta))\Rightarrow\varepsilon=\beta$;
同理可得$\alpha=\gamma$,$\beta=\delta$,$\gamma=\varepsilon$,
$\therefore\alpha=\beta=\gamma=\delta=\varepsilon$,即各弧相等。
$\because$同圆中相等弧所对弦相等,$\therefore AB=BC=CD=DE=EA$。
又$\angle A=\angle B=\angle C=\angle D=\angle E$,
$\therefore$五边形$ABCDE$是正五边形。
【针对训练】
1. 如图 24.3 - 2,$ \triangle ABC $ 是 $ \odot O $ 的内接等腰三角形,$ \angle BAC = 36^{\circ} $,弦 $ BD $,$ CE $ 分别平分 $ \angle ABC $,$ \angle ACB $。
求证:五边形 $ AEBCD $ 是正五边形。
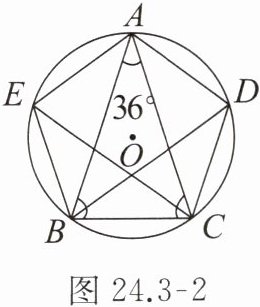
1. 如图 24.3 - 2,$ \triangle ABC $ 是 $ \odot O $ 的内接等腰三角形,$ \angle BAC = 36^{\circ} $,弦 $ BD $,$ CE $ 分别平分 $ \angle ABC $,$ \angle ACB $。
求证:五边形 $ AEBCD $ 是正五边形。

答案:
证明:
∵△ABC是等腰三角形,∠BAC=36°,
∴∠ABC=∠ACB=(180°-36°)/2=72°。
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠DBC=∠ABC/2=36°,∠ACE=∠ECB=∠ACB/2=36°。
∵∠BAC=36°(圆周角),所对弧BC,
∴弧BC=2∠BAC=72°(圆周角定理)。
∵∠DBC=36°(圆周角),所对弧CD,
∴弧CD=2∠DBC=72°。
∵∠ECB=36°(圆周角),所对弧EB,
∴弧EB=2∠ECB=72°。
∵∠ACE=36°(圆周角),所对弧AE,
∴弧AE=2∠ACE=72°。
∵圆的周角为360°,
∴弧DA=360°-弧AE-弧EB-弧BC-弧CD=360°-72°×4=72°。
∴弧AE=弧EB=弧BC=弧CD=弧DA=72°。
∴AE=EB=BC=CD=DA(同圆中,等弧对等弦)。
∵五边形AEBCD内接于⊙O,且各边所对弧相等,
∴各内角所对优弧度数=360°-2×72°=216°,
∴各内角=1/2×216°=108°(圆周角定理)。
∴五边形AEBCD各边相等,各角相等,
即五边形AEBCD是正五边形。
∵△ABC是等腰三角形,∠BAC=36°,
∴∠ABC=∠ACB=(180°-36°)/2=72°。
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠DBC=∠ABC/2=36°,∠ACE=∠ECB=∠ACB/2=36°。
∵∠BAC=36°(圆周角),所对弧BC,
∴弧BC=2∠BAC=72°(圆周角定理)。
∵∠DBC=36°(圆周角),所对弧CD,
∴弧CD=2∠DBC=72°。
∵∠ECB=36°(圆周角),所对弧EB,
∴弧EB=2∠ECB=72°。
∵∠ACE=36°(圆周角),所对弧AE,
∴弧AE=2∠ACE=72°。
∵圆的周角为360°,
∴弧DA=360°-弧AE-弧EB-弧BC-弧CD=360°-72°×4=72°。
∴弧AE=弧EB=弧BC=弧CD=弧DA=72°。
∴AE=EB=BC=CD=DA(同圆中,等弧对等弦)。
∵五边形AEBCD内接于⊙O,且各边所对弧相等,
∴各内角所对优弧度数=360°-2×72°=216°,
∴各内角=1/2×216°=108°(圆周角定理)。
∴五边形AEBCD各边相等,各角相等,
即五边形AEBCD是正五边形。
二、正多边形的有关计算
【例 2】如图 24.3 - 3,$ \odot O $ 是正六边形 $ ABCDEF $ 的外接圆,$ \odot O $ 的半径是 2,求正六边形 $ ABCDEF $ 的面积。
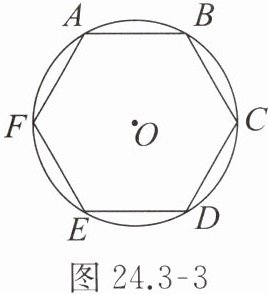
解:
【例 2】如图 24.3 - 3,$ \odot O $ 是正六边形 $ ABCDEF $ 的外接圆,$ \odot O $ 的半径是 2,求正六边形 $ ABCDEF $ 的面积。

解:
答案:
连接 $OA$,$OB$,并作 $OM\perp AB$ 于点 $M$。
$\because \odot O$的半径是$2$,
$\therefore OA = OB = 2$。
$\because$多边形$ABCDEF$为正六边形,
$\therefore \angle AOB = 60^{\circ}$,
$\therefore \triangle AOB$是等边三角形,
$\therefore AB = OA = 2$。
$\because OM\perp AB$,$OA = 2$,
$\therefore OM = \sqrt{OA^{2} - (\frac{AB}{2})^{2}} = \sqrt{3}$,
$\therefore S_{\triangle AOB} = \frac{1}{2} × AB × OM = \sqrt{3}$。
$\because$正六边形 $ABCDEF$ 的面积等于 $6S_{\triangle AOB}$,
$\therefore$正六边形 $ABCDEF$ 的面积为 $6\sqrt{3}$。
$\because \odot O$的半径是$2$,
$\therefore OA = OB = 2$。
$\because$多边形$ABCDEF$为正六边形,
$\therefore \angle AOB = 60^{\circ}$,
$\therefore \triangle AOB$是等边三角形,
$\therefore AB = OA = 2$。
$\because OM\perp AB$,$OA = 2$,
$\therefore OM = \sqrt{OA^{2} - (\frac{AB}{2})^{2}} = \sqrt{3}$,
$\therefore S_{\triangle AOB} = \frac{1}{2} × AB × OM = \sqrt{3}$。
$\because$正六边形 $ABCDEF$ 的面积等于 $6S_{\triangle AOB}$,
$\therefore$正六边形 $ABCDEF$ 的面积为 $6\sqrt{3}$。
【针对训练】
2. 如图 24.3 - 4,等边三角形 $ ABC $ 的外接圆 $ \odot O $ 的半径为 $ R $,求等边三角形 $ ABC $ 的边长、边心距、周长和面积。
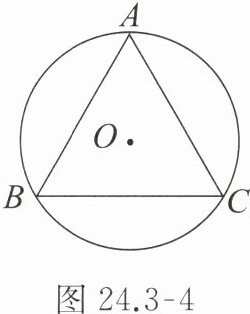
2. 如图 24.3 - 4,等边三角形 $ ABC $ 的外接圆 $ \odot O $ 的半径为 $ R $,求等边三角形 $ ABC $ 的边长、边心距、周长和面积。

答案:
边长√3 R,边心距R/2,周长3√3 R,面积3√3 R²/4。
查看更多完整答案,请扫码查看


