《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

1. 点 $ O $ 到直线 $ AB $ 的距离为 $ 4 cm $,以 $ 3\sqrt{2} cm $ 为半径的 $ \odot O $ 与直线 $ AB $ 的位置关系是(A)
A.相交
B.相切
C.相离
D.不能确定

答案： A

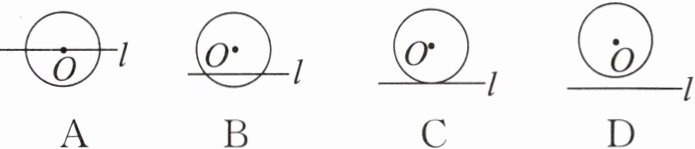
2. 已知 $ \odot O $ 的半径为 $ 5 $,圆心 $ O $ 到直线 $ l $ 的距离为 $ 3 $,则反映直线 $ l $ 与 $ \odot O $ 的位置关系的图形是(A)

 

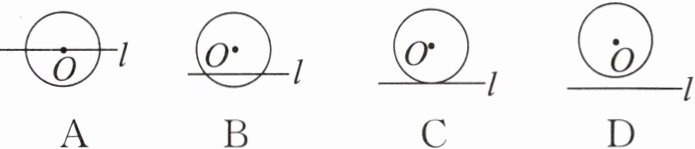
答案： A

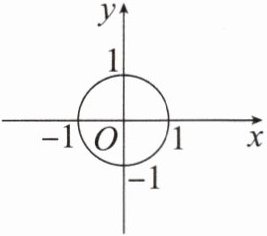
3. 如图 24.2.2 - 2,在平面直角坐标系中,$ \odot O $ 的半径为 $ 1 $,则直线 $ y = x - \sqrt{2} $ 与 $ \odot O $ 的位置关系是(B)

A.相离
B.相切
C.相交
D.以上三种情况都有可能

答案： B

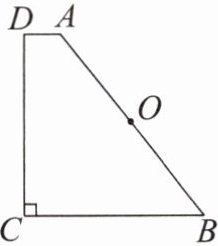
4. 如图 24.2.2 - 3,在直角梯形 $ ABCD $ 中,$ AD // BC $,$ \angle C = 90° $,且 $ AB ＞ AD + BC $,$ AB $ 是 $ \odot O $ 的直径,则直线 $ CD $ 与 $ \odot O $ 的位置关系为(C)

A.相离
B.相切
C.相交
D.无法确定

答案： C

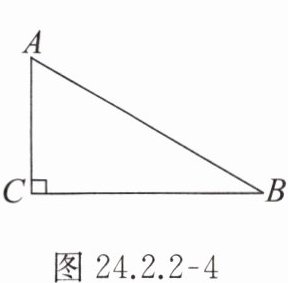
5. 如图 24.2.2 - 4,在 $ Rt \triangle ABC $ 中,$ \angle C = 90° $,$ \angle A = 60° $,$ BC = 4 cm $,以点 $ C $ 为圆心,以 $ 3 cm $ 长为半径作圆,则 $ \odot C $ 与直线 $ AB $ 的位置关系是相交。
 

答案： 相交

6. 如图 24.2.2 - 5,$ \odot A $ 的圆心坐标为 $ (0, 4) $,若 $ \odot A $ 的半径为 $ 3 $,则直线 $ y = x $ 与 $ \odot A $ 的位置关系是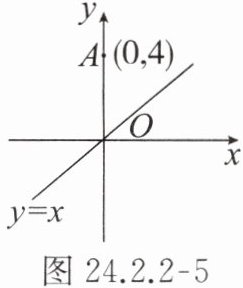相交。

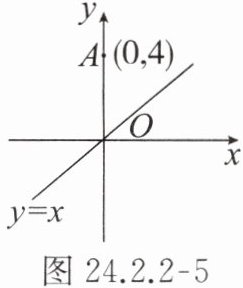
答案： 相交（题目要求直接填写关系，一般相交，相切，相离为该题三种答案，本题填“相交”）

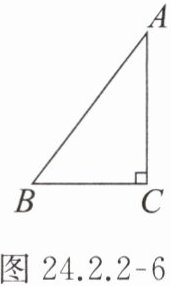
7. 如图 24.2.2 - 6,在 $ Rt \triangle ABC $ 中,$ AB = 10 cm $,$ BC = 6 cm $,$ AC = 8 cm $,则当 $ r $ 的取值为下列 $ 3 $ 种情况时,以点 $ C $ 为圆心,$ r $ 为半径的 $ \odot C $ 与直线 $ AB $ 有怎样的位置关系？
(1) $ r = 4 cm $；

(2) $ r = 4.8 cm $；
(3) $ r = 6 cm $。

答案： 过点$C$作$CD \perp AB$于点$D$。
在$Rt\triangle ABC$中，$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，即$\frac{1}{2}×8×6=\frac{1}{2}×10× CD$，解得$CD = 4.8\space cm$。
(1) 当$r = 4\space cm$时，$r\lt CD$，$\odot C$与直线$AB$相离。
(2) 当$r = 4.8\space cm$时，$r = CD$，$\odot C$与直线$AB$相切。
(3) 当$r = 6\space cm$时，$r\gt CD$，$\odot C$与直线$AB$相交。