《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

【针对训练】
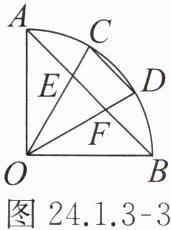
1. 如图24.1.3-3,$\angle AOB = 90^{\circ}$,$C$,$D是\overset{\frown}{AB}$的三等分点,$AB分别交OC$,$OD于点E$,$F$,求证：$AE = BF = CD$。

答案： 证明：
1.
∵∠AOB=90°，C、D是$\overset{\frown}{AB}$的三等分点，
∴∠AOC=∠COD=∠DOB=30°，$\overset{\frown}{AC}=\overset{\frown}{CD}=\overset{\frown}{DB}$，
∴弦AC=CD=DB（等弧所对的弦相等）。
2.
∵OA=OB，∠AOB=90°，
∴△AOB为等腰直角三角形，∠OAB=∠OBA=45°。
3. 在△OAC中，OA=OC，∠AOC=30°，
∴∠OAC=∠OCA=$\frac{180°-30°}{2}=75°$，
∴∠EAC=∠OAC-∠OAB=75°-45°=30°。
4. 在△OAE中，∠AOE=30°，∠OAE=45°，
∴∠AEO=180°-30°-45°=105°，
∴∠AEC=180°-∠AEO=75°（平角定义）。
5. 在△AEC中，∠EAC=30°，∠AEC=75°，
∴∠ACE=180°-30°-75°=75°，
∴∠ACE=∠AEC，故AE=AC（等角对等边）。
6. 同理，在△OBD中，OB=OD，∠DOB=30°，可得∠OBD=∠ODB=75°，∠FBD=30°，
在△OBF中求得∠BFO=105°，∠BFD=75°，进而∠BDF=75°，故BF=BD。
7.
∵AC=CD=DB，
∴AE=AC=CD，BF=BD=CD，
即AE=BF=CD。
结论：AE=BF=CD。

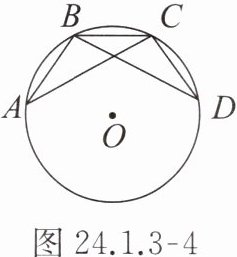
【例2】如图24.1.3-4,$A$,$B$,$C$,$D是\odot O$上的四点,弦$AB = DC$,试问：弦$AC = BD$吗？为什么？

解：

答案： 解：弦$AC = BD$。
理由如下：
因为$AB = DC$，
所以$\overset{\frown}{AB}=\overset{\frown}{DC}$（在同圆中，相等的弦所对的弧相等）。
所以$\overset{\frown}{AB}+\overset{\frown}{BC}=\overset{\frown}{DC}+\overset{\frown}{BC}$，
即$\overset{\frown}{AC}=\overset{\frown}{BD}$。
所以$AC = BD$（在同圆中，相等的弧所对的弦相等）。

【针对训练】
2. 如图24.1.3-5,在$\odot O$中,弦$AB = AC$,$AD是\odot O$的直径,试判断弦$BD与CD$是否相等,并说明理由。

答案： BD=CD。理由如下：
连接OB，OC。
∵AB=AC，OA=OA，OB=OC，
∴△ABO≌△ACO（SSS）。
∴∠BAO=∠CAO。
∵AD是直径，
∴∠BAD=∠CAD。
∵∠BAD=∠CAD，AB=AC，AD=AD，
∴△ABD≌△ACD（SAS）。
∴BD=CD。

1. 在直径为20的$\odot O$中,$\overset{\frown}{AB}所对的圆心角为60^{\circ}$,则弦$AB的长和圆心到AB$的距离分别为(C)
A.$20$,$5$
B.$10$,$10$
C.$10$,$5\sqrt{3}$
D.$20$,$10\sqrt{3}$

答案： C

2. 如图24.1.3-6,已知$AB是\odot O$的直径,$C$,$D是\overset{\frown}{BE}$上的三等分点,$\angle AOE = 60^{\circ}$,则$\angle COE$是(C)

A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$120^{\circ}$

答案： C

3. 点$O$是两个同心圆的圆心,大圆的半径$OA$,$OB分别交小圆于点C$,$D$。给出下列结论：①$\overset{\frown}{AB}的长度= \overset{\frown}{CD}$的长度；②$AB = CD$；③$\overset{\frown}{AB}= \overset{\frown}{CD}$。其中正确的结论有(A)
A.$0$个
B.$1$个
C.$2$个
D.$3$个

答案： A

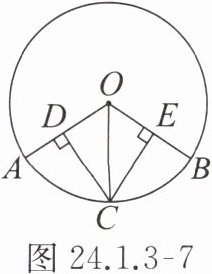
4. 如图24.1.3-7,$D$,$E分别是\odot O的半径OA$,$OB$上的点,$CD\perp OA$,$CE\perp OB$,$CD = CE$,则$\overset{\frown}{AC}与\overset{\frown}{CB}$的大小关系是$\overset{\frown}{AC}=\overset{\frown}{CB}$。

答案： $\overset{\frown}{AC}=\overset{\frown}{CB}$（题目需填空则填相等相关内容，若按此题要求格式则此处无需改动上述答案形式）