《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

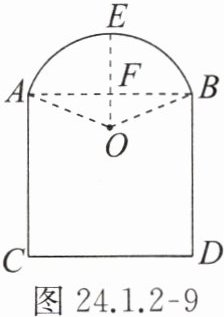
7. 如图 24.1.2 - 9 所示,某窗户由矩形和弓形组成,已知弓形的跨度 AB = 3 m,弓形的高 EF = 1 m,现计划安装玻璃,请帮工程师求出$\overset{\frown}{AB}$所在圆 O 的半径 r。

答案： 根据题意，设$\odot O$的半径为$r$，$AB = 3m$，$EF = 1m$，$F$为$AB$中点，则$AF=\frac{3}{2}m$，$OF = r - 1$。
在$Rt\triangle AOF$中，由勾股定理$OA^{2}=AF^{2}+OF^{2}$，即$r^{2}=(\frac{3}{2})^{2}+(r - 1)^{2}$。
展开得$r^{2}=\frac{9}{4}+r^{2}-2r + 1$。
移项可得$2r=\frac{9}{4}+1$，$2r=\frac{13}{4}$，解得$r = \frac{13}{8}=1.625m$。
答：$\overset{\frown}{AB}$所在圆$O$的半径$r$为$1.625m$。

8. 已知 AB,CD 是$\odot O$的两条弦,$\odot O$的半径为 10 cm,且 AB $//$ CD,AB = 16 cm,CD = 12 cm,试求出两弦 AB,CD 的距离。

答案： 情况1：两弦在圆心同侧
过O作OE⊥AB于E，OF⊥CD于F，连接OA，OC。
由垂径定理得：AE=AB/2=8cm，CF=CD/2=6cm。
在Rt△AOE中，OE²+AE²=OA²，OE²=10²-8²=36，OE=6cm。
在Rt△COF中，OF²+CF²=OC²，OF²=10²-6²=64，OF=8cm。
距离=OF-OE=8-6=2cm。
情况2：两弦在圆心两侧
距离=OE+OF=6+8=14cm。
综上，两弦距离为2cm或14cm。

【例1】下列说法正确吗？
(1)如图24.1.3-1,小明说：“因为$\overset{\frown}{AB}和\overset{\frown}{A'B'}所对的圆心角都是\angle O$,所以$\overset{\frown}{AB}= \overset{\frown}{A'B'}$”；
(2)如图24.1.3-2,小华说：“因为$AB = CD$,故$AB所对的\overset{\frown}{AB}等于CD所对的\overset{\frown}{CAD}$”。
解：

答案：
(1)不正确。理由：$\overset{\frown}{AB}$与$\overset{\frown}{A'B'}$所在圆的半径不同（非等圆），虽圆心角相等，但所对弧不相等。
(2)不正确。理由：$AB=CD$只能推出它们所对的劣弧（或优弧）相等，而$\overset{\frown}{CAD}$是优弧，$\overset{\frown}{AB}$未明确是否为优弧，二者不一定相等。