第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 将图 23.1 - 5 中的图按顺时针方向旋转 $90^{\circ}$ 后得到的是(

A
)
答案:
A
2. 如图 23.1 - 6,将 $Rt\triangle ABC$(其中 $\angle B = 35^{\circ}$,$\angle C = 90^{\circ}$)绕点 $A$ 按顺时针方向旋转到 $\triangle AB_{1}C_{1}$ 的位置,使得点 $C$,$A$,$B_{1}$ 在同一条直线上,那么旋转角等于(
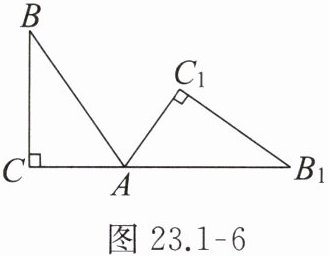
A.$55^{\circ}$
B.$70^{\circ}$
C.$125^{\circ}$
D.$145^{\circ}$
C
)
A.$55^{\circ}$
B.$70^{\circ}$
C.$125^{\circ}$
D.$145^{\circ}$
答案:
C
3. 如图 23.1 - 7,在 $6×4$ 方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则旋转中心是(
A.格点 $M$
B.格点 $N$
C.格点 $P$
D.格点 $Q$
B
)
A.格点 $M$
B.格点 $N$
C.格点 $P$
D.格点 $Q$
答案:
B
4. 如图 23.1 - 8,把 $Rt\triangle ABC$ 绕点 $A$ 逆时针旋转 $40^{\circ}$,得到 $Rt\triangle AB'C'$,点 $C'$ 恰好落在边 $AB$ 上,连接 $BB'$,则 $\angle BB'C' = $

20°
。
答案:
20°
5. 如图 23.1 - 9 所示,在正方形 $ABCD$ 中,$E$ 是正方形内的一点,把 $\triangle AED$ 绕点 $A$ 按逆时针方向旋转 $90^{\circ}$,得到 $\triangle AE'B$,观察并回答:
(1)图中有哪些相等的线段与相等的角?
(2)哪两个三角形的形状、大小一样?

(1)图中有哪些相等的线段与相等的角?
(2)哪两个三角形的形状、大小一样?

答案:
(1)相等的线段:
$AD = AB$,$AE = AE'$,$DE = BE'$。
相等的角:
$\angle DAB = \angle EAE' = 90^{\circ}$,$\angle ADE = \angle ABE'$,$\angle DAE = \angle BAE'$,$\angle DEA = \angle BE'A$。
(2)$\triangle ADE$和$\triangle ABE'$的形状、大小一样。
(1)相等的线段:
$AD = AB$,$AE = AE'$,$DE = BE'$。
相等的角:
$\angle DAB = \angle EAE' = 90^{\circ}$,$\angle ADE = \angle ABE'$,$\angle DAE = \angle BAE'$,$\angle DEA = \angle BE'A$。
(2)$\triangle ADE$和$\triangle ABE'$的形状、大小一样。
6. 如图 23.1 - 10,每个小方格都是边长为 1 个单位长度的小正方形。
(1)将 $\triangle ABC$ 向右平移 3 个单位长度,画出平移后的 $\triangle A_{1}B_{1}C_{1}$;
(2)将 $\triangle ABC$ 绕点 $O$ 旋转 $180^{\circ}$,画出旋转后的 $\triangle A_{2}B_{2}C_{2}$;
(3)连接 $AC_{1}$,$C_{1}A_{2}$,$A_{2}A$,过点 $O$ 画出一条直线将 $\triangle AC_{1}A_{2}$ 的面积分成相等的两部分。
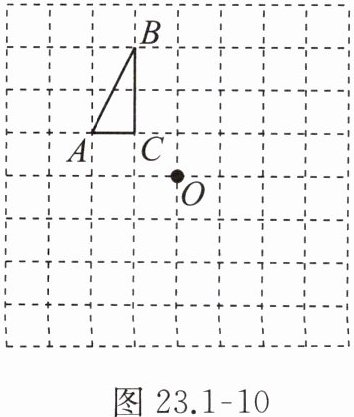
(1)将 $\triangle ABC$ 向右平移 3 个单位长度,画出平移后的 $\triangle A_{1}B_{1}C_{1}$;
(2)将 $\triangle ABC$ 绕点 $O$ 旋转 $180^{\circ}$,画出旋转后的 $\triangle A_{2}B_{2}C_{2}$;
(3)连接 $AC_{1}$,$C_{1}A_{2}$,$A_{2}A$,过点 $O$ 画出一条直线将 $\triangle AC_{1}A_{2}$ 的面积分成相等的两部分。

答案:
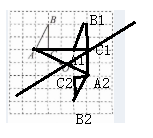

查看更多完整答案,请扫码查看


