第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
【例 1】如图 23.1 - 1,在 $Rt\triangle OAB$ 中,$\angle OAB = 90^{\circ}$,$OA = AB = 6$,将 $\triangle OAB$ 绕点 $O$ 沿逆时针方向旋转 $90^{\circ}$ 得到 $\triangle OA_{1}B_{1}$。

(1)线段 $OA_{1}$ 的长是
(2)$\angle AOB_{1}$ 的度数是
(3)连接 $AA_{1}$,求证:四边形 $OAA_{1}B_{1}$ 是平行四边形;
(4)求四边形 $OAA_{1}B_{1}$ 的面积。
解:

(1)线段 $OA_{1}$ 的长是
6
;(2)$\angle AOB_{1}$ 的度数是
135°
;(3)连接 $AA_{1}$,求证:四边形 $OAA_{1}B_{1}$ 是平行四边形;
(4)求四边形 $OAA_{1}B_{1}$ 的面积。
解:
(3) 证明:∵△OAB绕点O逆时针旋转90°得到△OA₁B₁,∴OA₁=OA,A₁B₁=AB,∠OA₁B₁=∠OAB=90°,∠AOA₁=90°。
∵在Rt△OAB中,OA=AB=6,∠OAB=90°,∴A₁B₁=AB=OA。
∵∠AOA₁=90°,∠OA₁B₁=90°,∴OA⊥OA₁,A₁B₁⊥OA₁,∴OA//A₁B₁。
又∵OA=A₁B₁,∴四边形OAA₁B₁是平行四边形。
(4) 36
∵在Rt△OAB中,OA=AB=6,∠OAB=90°,∴A₁B₁=AB=OA。
∵∠AOA₁=90°,∠OA₁B₁=90°,∴OA⊥OA₁,A₁B₁⊥OA₁,∴OA//A₁B₁。
又∵OA=A₁B₁,∴四边形OAA₁B₁是平行四边形。
(4) 36
答案:
(1) 6
(2) 135°
(3) 证明:
∵△OAB绕点O逆时针旋转90°得到△OA₁B₁,
∴OA₁=OA,A₁B₁=AB,∠OA₁B₁=∠OAB=90°,∠AOA₁=90°。
∵在Rt△OAB中,OA=AB=6,∠OAB=90°,
∴A₁B₁=AB=OA。
∵∠AOA₁=90°,∠OA₁B₁=90°,
∴OA⊥OA₁,A₁B₁⊥OA₁,
∴OA//A₁B₁。
又
∵OA=A₁B₁,
∴四边形OAA₁B₁是平行四边形。
(4) 36
(1) 6
(2) 135°
(3) 证明:
∵△OAB绕点O逆时针旋转90°得到△OA₁B₁,
∴OA₁=OA,A₁B₁=AB,∠OA₁B₁=∠OAB=90°,∠AOA₁=90°。
∵在Rt△OAB中,OA=AB=6,∠OAB=90°,
∴A₁B₁=AB=OA。
∵∠AOA₁=90°,∠OA₁B₁=90°,
∴OA⊥OA₁,A₁B₁⊥OA₁,
∴OA//A₁B₁。
又
∵OA=A₁B₁,
∴四边形OAA₁B₁是平行四边形。
(4) 36
【针对训练】
1. 如图 23.1 - 2,将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $40^{\circ}$ 得 $\triangle A'CB'$,若 $AC\perp A'B'$,则 $\angle A = $(

A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
1. 如图 23.1 - 2,将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $40^{\circ}$ 得 $\triangle A'CB'$,若 $AC\perp A'B'$,则 $\angle A = $(
A
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
A
二、旋转作图
【例 2】如图 23.1 - 3,$O$ 是 $Rt\triangle ABC$ 外一点,试作出 $Rt\triangle ABC$ 绕点 $O$ 按顺时针旋转 $180^{\circ}$ 后的图形。

【例 2】如图 23.1 - 3,$O$ 是 $Rt\triangle ABC$ 外一点,试作出 $Rt\triangle ABC$ 绕点 $O$ 按顺时针旋转 $180^{\circ}$ 后的图形。

答案:
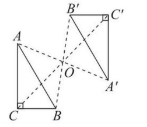

【针对训练】
2. 如图 23.1 - 4,作出 $\triangle ABC$ 绕点 $O$ 顺时针旋转 $60^{\circ}$ 后的三角形。

2. 如图 23.1 - 4,作出 $\triangle ABC$ 绕点 $O$ 顺时针旋转 $60^{\circ}$ 后的三角形。

答案:
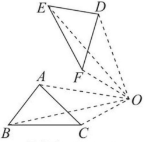

查看更多完整答案,请扫码查看


