《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

【例 2】将一根长为 $ 16\pi cm $ 的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为 $ r_1 $(单位：$cm$)和 $ r_2 $(单位：$cm$).
(1)求 $ r_1 $ 与 $ r_2 $ 的关系式,并写出 $ r_1 $ 的取值范围；
(2)将两圆的面积之和 $ S $ 表示成 $ r_1 $ 的函数关系式,并求出 $ S $ 的最小值.
解：

答案：
(1) $r_2 = 8 - r_1$，$0 ＜ r_1 ＜ 8$；
(2) $S = 2\pi r_1^2 - 16\pi r_1 + 64\pi$，最小值为 $32\pi\ cm^2$。

【针对训练】
2.小磊要制作一个三角形的钢架模型,在这个三角形中,长度为 $ x $(单位：$cm$)的边与这条边上的高之和为 $ 40 cm $,这个三角形的面积为 $ S $(单位：$cm^2$).
(1)请直接写出 $ S $ 与 $ x $ 之间的函数关系式(不要求写出自变量 $ x $ 的取值范围).
(2)当 $ x $ 是多少时,这个三角形面积 $ S $ 最大？最大面积是多少？

答案：
(1)
设长度为$x$ $cm$的边上的高为$h$ $cm$，
由题意得$x + h = 40$，即$h = 40 - x$。
根据三角形面积公式$S=\frac{1}{2}×$底$×$高，
可得$S=\frac{1}{2}x(40 - x)=- \frac{1}{2}x^{2}+20x$。
(2)
对于二次函数$S = - \frac{1}{2}x^{2}+20x$，其中$a = - \frac{1}{2}$，$b = 20$，$c = 0$。
根据二次函数性质，当$x = -\frac{b}{2a}=-\frac{20}{2×(-\frac{1}{2})}= 20$时，
$S$有最大值，$S_{最大值}=\frac{4ac - b^{2}}{4a}=\frac{0 - 20^{2}}{4×(-\frac{1}{2})}=200$ $cm^{2}$。
答：
(1)$S = - \frac{1}{2}x^{2}+20x$；
(2)当$x = 20$时，$S$最大，最大面积是$200$ $cm^{2}$。

1.为搞好环保,某公司准备修建一个长方体的污水处理池,若矩形池底的周长为 $ 100 m $,则池底的最大面积是(B)
A.$ 600 m^2 $
B.$ 625 m^2 $
C.$ 650 m^2 $
D.$ 675 m^2 $

答案： B

2.某旅行团要接团去外地旅游,经计算所获营业额 $ y $(单位：元)与旅行团人数 $ x $(单位：人)满足关系式 $ y = -x^2 + 100x + 28400 $,要使所获营业额最大,则此旅行团应有(C)
A.30 人
B.40 人
C.50 人
D.55 人

答案： C

3.将进货单价为 70 元的某种商品按零售价 100 元售出时,每天能卖出 20 个,若这种商品零售价在一定范围内每降价 1 元,其日销售量就增加 1 个,为获得最大利润,应降价(A)
A.5 元
B.10 元
C.15 元
D.20 元

答案： A

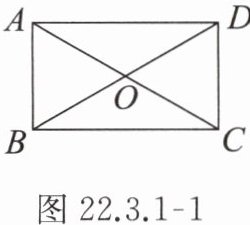
4. 如图 22.3.1 - 1,矩形 $ ABCD $ 的两对角线 $ AC $,$ BD $ 交于点 $ O $,$ \angle AOB = 60° $,设 $ AB = x cm $,矩形 $ ABCD $ 的面积为 $ S cm^2 $,则 $ S $ 与 $ x $ 之间的函数关系式为(A)

A.$ S = \sqrt{3}x^2 $
B.$ S = \frac{\sqrt{3}}{3}x^2 $
C.$ S = \frac{\sqrt{3}}{2}x^2 $
D.$ S = \frac{1}{2}x^2 $

答案： A

5.某广告设计公司承接一项业务：设计一幅周长为 12 米的矩形广告牌,广告设计费为 1000 元/平方米,则获得的设计费最多是9000元.

答案： 9000