第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
【例 1】某校学生积极参与“保护濒危动物”的活动,他们购进一批单价为 20 元的“文化衫”,在课余时间进行义卖.在义卖过程中发现,若每件按 24 元的价格销售时,每天能卖出 36 件;若每件按 29 元的价格销售时,每天能卖出 21 件.假定每天销售数量 $ y $(单位:件)与销售价格 $ x $(单位:元/件)满足一个以 $ x $ 为自变量的一次函数.
(1)求 $ y $ 与 $ x $ 满足的函数关系式(不要求写出 $ x $ 的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少时,才能使每天获得的利润 $ P $ 最大?
解:
(1)求 $ y $ 与 $ x $ 满足的函数关系式(不要求写出 $ x $ 的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少时,才能使每天获得的利润 $ P $ 最大?
解:
答案:
(1) 设销售数量 $y$ 与销售价格 $x$ 的关系为线性函数 $y = kx + b$。
根据题意,有以下方程组:
$\begin{cases}24k + b = 36, \\29k + b = 21.\end{cases}$
解这个方程组,得到:
$\begin{cases}k = -3, \\b = 108.\end{cases}$
因此,销售数量 $y$ 与销售价格 $x$ 的函数关系式为 $y = -3x + 108$。
(2) 根据题意,每天获得的利润 $P$ 可以表示为:
$P = (x - 20)(-3x + 108) = -3x^2 + 168x - 2160= -3(x - 28)^2 + 192$
由于 $a = -3 < 0$,这是一个开口向下的抛物线,因此当 $x = 28$ 时,$P$ 取得最大值。
所以销售价格定为 $28$ 元/件时,每天获得的利润 $P$ 最大。
(1) 设销售数量 $y$ 与销售价格 $x$ 的关系为线性函数 $y = kx + b$。
根据题意,有以下方程组:
$\begin{cases}24k + b = 36, \\29k + b = 21.\end{cases}$
解这个方程组,得到:
$\begin{cases}k = -3, \\b = 108.\end{cases}$
因此,销售数量 $y$ 与销售价格 $x$ 的函数关系式为 $y = -3x + 108$。
(2) 根据题意,每天获得的利润 $P$ 可以表示为:
$P = (x - 20)(-3x + 108) = -3x^2 + 168x - 2160= -3(x - 28)^2 + 192$
由于 $a = -3 < 0$,这是一个开口向下的抛物线,因此当 $x = 28$ 时,$P$ 取得最大值。
所以销售价格定为 $28$ 元/件时,每天获得的利润 $P$ 最大。
【针对训练】
1.某产品每件的成本为 10 元,试销阶段该产品的销售单价 $ x $(单位:元)与产品的日销售量 $ y $(单位:件)之间的关系如下表:
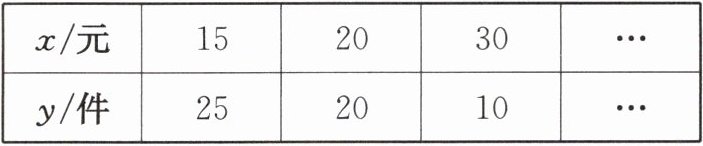
已知日销售量 $ y $ 是销售单价 $ x $ 的一次函数.
(1)求出日销售量 $ y $(单位:件)与销售单价 $ x $(单位:元)的函数关系式.
(2)要使每日的销售利润最大,每件产品的销售单价应定为多少元?此时每日销售利润是多少元?
1.某产品每件的成本为 10 元,试销阶段该产品的销售单价 $ x $(单位:元)与产品的日销售量 $ y $(单位:件)之间的关系如下表:

已知日销售量 $ y $ 是销售单价 $ x $ 的一次函数.
(1)求出日销售量 $ y $(单位:件)与销售单价 $ x $(单位:元)的函数关系式.
(2)要使每日的销售利润最大,每件产品的销售单价应定为多少元?此时每日销售利润是多少元?
答案:
(1) 设函数关系式为 $y = kx + b$。
代入点 $(15, 25)$ 和 $(20, 20)$ 到 $y = kx + b$,得到方程组:
$\begin{cases}15k + b = 25, \\20k + b = 20.\end{cases}$
解得$k = -1$,$b = 40$。
因此,日销售量 $y$ 与销售单价 $x$ 的函数关系式为 $y = -x + 40$。
(2) 设每日销售利润为 $w$ 元。则
$w = (x - 10)(-x + 40)$
$ = -x^2 + 50x - 400 $
$ = -(x - 25)^2 + 225$
由于二次项系数为负,这是一个开口向下的抛物线,因此当 $x = 25$ 时,$w$ 取得最大值,即 $225$ 元。
答:要使每日销售利润最大,每件产品的销售单价应定为 $25$ 元,此时每日销售利润是 $225$ 元。
(1) 设函数关系式为 $y = kx + b$。
代入点 $(15, 25)$ 和 $(20, 20)$ 到 $y = kx + b$,得到方程组:
$\begin{cases}15k + b = 25, \\20k + b = 20.\end{cases}$
解得$k = -1$,$b = 40$。
因此,日销售量 $y$ 与销售单价 $x$ 的函数关系式为 $y = -x + 40$。
(2) 设每日销售利润为 $w$ 元。则
$w = (x - 10)(-x + 40)$
$ = -x^2 + 50x - 400 $
$ = -(x - 25)^2 + 225$
由于二次项系数为负,这是一个开口向下的抛物线,因此当 $x = 25$ 时,$w$ 取得最大值,即 $225$ 元。
答:要使每日销售利润最大,每件产品的销售单价应定为 $25$ 元,此时每日销售利润是 $225$ 元。
查看更多完整答案,请扫码查看


