《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

6. 在一幅长为 80 cm、宽为 50 cm 的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图 21.3.2 - 4 所示.如果要使整个挂图的面积是$ 5400 cm^2,$设金色纸边的宽为 x cm,那么 x 满足的方程是$(80 + 2x)(50 + 2x) = 5400$.

答案： $(80 + 2x)(50 + 2x) = 5400$（写成标准方程形式也可）

7. 有一间长 20 m、宽 15 m 的会议室,在它的中间铺一块地毯,地毯的面积是会议室地面面积的一半,四周未铺地毯的留空宽度相同,则留空宽度为2.5m.

答案： 2.5

8. 某两位数的十位数字与个位数字之和是 5,把这个数的个位数字与十位数字对调后,所得的新两位数与原两位数的乘积为 736,求原来的两位数.

答案： 设原来的两位数的十位数字为 $x$，则个位数字为 $5 - x$。
原来的两位数可以表示为：$10x + (5 - x) = 9x + 5$（数字表示法，十位乘以10加个位）。
对调后的两位数可以表示为：$10(5 - x) + x = 50 - 9x$。
根据题意，这两个数的乘积为736，即：
$(9x + 5)(50 - 9x) = 736$
展开并整理得：
$450x - 81x^2 + 250 - 45x = 736$
$-81x^2 + 405x - 486 = 0$
$x^2 - 5x + 6 = 0$
解这个一元二次方程，得到：
$(x - 2)(x - 3) = 0$
$x_1 = 2, \quad x_2 = 3$
当 $x = 2$ 时，个位数字为 $5 - 2 = 3$，原来的两位数为 $23$。
当 $x = 3$ 时，个位数字为 $5 - 3 = 2$，原来的两位数为 $32$。
故原来的两位数为 $23$ 或 $32$。

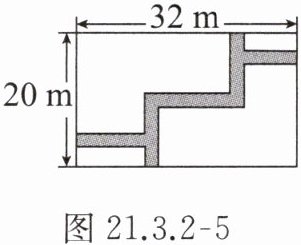
9. 如图 21.3.2 - 5,在宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为$ 540 m^2,$求道路的宽.

答案： 设道路的宽为$ x $米。
矩形地面总面积：$ 32 × 20 = 640 \, m^2 $。
草坪面积为$ 540 \, m^2 $，将道路平移后，草坪部分形成一个新矩形，其长为$ (32 - x) \, m $，宽为$ (20 - x) \, m $。
根据题意，得：$ (32 - x)(20 - x) = 540 $。
展开并整理：$ x^2 - 52x + 100 = 0 $。
解方程：$ x = \frac{52 \pm \sqrt{52^2 - 4 × 1 × 100}}{2} = \frac{52 \pm 48}{2} $。
解得：$ x_1 = 50 $（舍去，不合题意），$ x_2 = 2 $。
答：道路的宽为$ 2 \, m $。

10. 如图 21.3.2 - 6,已知在△ABC 中,∠B = 90°,AB = 5 cm,BC = 7 cm,点 P 从点 A 开始沿边 AB 向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 开始沿边 BC 向点 C 以 2 cm/s 的速度移动.
(1)如果 P,Q 分别从 A,B 同时出发,那么几秒后,△PBQ 的面积等于$ 4 cm^2？$
(2)如果 P,Q 分别从 A,B 同时出发,那么几秒后,PQ 的长度等于 5 cm？
(3)如果 P,Q 分别从 A,B 同时出发,△PQB 的面积能否等于$ 7 cm^2？$请说明理由.

答案：
(1)设$t$秒后，$\triangle PBQ$的面积等于$4cm^2$。
$AP = t cm$，$BP = (5 - t) cm$，$BQ = 2t cm$。
$S_{\triangle PBQ} =\frac{1}{2} × BP × BQ$
$4 = \frac{1}{2} × (5 - t) × 2t$
$4 = 5t - t^2$
$t^2 - 5t + 4 = 0$
$(t - 1)(t - 4) = 0$
$t_1 = 1, \quad t_2 = 4$
由于$0\leq t\leq 5$且$0 \leq 2t \leq 7$，即$0\leq t\leq 3.5$，
所以$t = 4$（舍去），
综上，$1$秒后，$\triangle PBQ$的面积等于$4cm^2$。
(2)设$t$秒后，$PQ$的长度等于$5cm$。
$BP = (5 - t) cm$，$BQ = 2t cm$。
$PQ = \sqrt{BP^2 + BQ^2}$
$5 = \sqrt{(5 - t)^2 + (2t)^2}$
$25 = 25 - 10t + t^2 + 4t^2$
$5t^2 - 10t = 0$
$5t(t - 2) = 0$
$t_1 = 0, \quad t_2 = 2$
由于$t = 0$时，$PQ$为$AB$，长度为$5cm$，但题目要求$P$和$Q$移动后的长度，所以$t = 0$舍去。
综上，$2$秒后，$PQ$的长度等于$5cm$。
(3)设$t$秒后，$\triangle PQB$的面积能等于$7cm^2$。
$AP = t cm$，$BP = (5 - t) cm$，$BQ = 2t cm$。
$S_{\triangle PQB} = \frac{1}{2} × BP × BQ$
$7 = \frac{1}{2} × (5 - t) × 2t$
$7 = 5t - t^2$
$t^2 - 5t + 7 = 0$
$\Delta = (-5)^2 - 4 × 1 × 7 = -3 ＜ 0$
由于判别式小于$0$，方程无实数解。
综上，$\triangle PQB$的面积不能等于$7cm^2$。