《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

9. 某山西特产专卖店销售核桃,其进价为 40 元/千克,按 60 元/千克出售,平均每天可售出 100 千克.后来经过市场调查发现,单价每降低 2 元,则平均每天的销售量可增加 20 千克.若该专卖店销售这种核桃要想平均每天获利 2240 元,请回答：
(1)每千克核桃应降价多少元？
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售？

答案：
(1) 设每千克核桃应降价$x$元。
原售价为60元/千克，进价为40元/千克，因此原利润为$60 - 40 = 20$(元/千克)。
降价后，售价为$60 - x$元/千克，利润为$20 - x$（这里$x$也代表每千克降价带来的利润减少） 元/（千克）（但实际上利润应计算为$(60 - x) - 40 = 20 - x$（元/千克）更准确，不过在此问题中，我们关注的是总利润）。
原销售量为100千克/天，每降价2元，销售量增加20千克。
因此，降价$x$元后，销售量为$100 + 10x$ 千克/天（因为每降价2元增加20千克，所以降价$x$元增加$\frac{x}{2} × 20 = 10x$ 千克）。
总利润为：$(20 - x)(100 + 10x)$。
根据题意，这个总利润应该等于2240元，所以我们有方程：
$(20 - x)(100 + 10x) = 2240$，
$2000 + 200x - 100x - 10x^2 = 2240$，
$-10x^2 + 100x - 240 = 0$，
$x^2 - 10x + 24 = 0$，
$(x - 4)(x - 6) = 0$，
解得：$x_1 = 4$，$x_2 = 6$。
答：每千克核桃应降价4元或6元。
(2) 由
(1)可知每千克核桃可降价4元或6元。
因为要尽可能让利于顾客，赢得市场，所以选择降价6元。
原售价为60元/千克，降价6元后，售价为54元/千克。
设按原售价的$y$折出售，则：
$60 × \frac{y}{10} = 54$，
解得：$y = 9$。
答：该店应按原售价的9折出售。

一、面积类问题
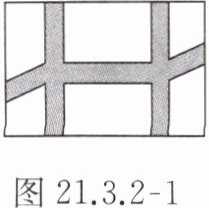
【例 1】为响应市委市政府提出的建设“绿色城市”的号召,某单位准备将院内一块长 30 m,宽 20 m 的长方形空地建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图 21.3.2 - 1 所示.要使种植花草的面积为$ 532 m^2,$那么小道进出口的宽度应为多少米？(注：所有小道进出口的宽度相等,且每段小道均为平行四边形)

解：

答案： 设小道进出口的宽度为$x$米。
根据题意和图形特征可知，种花草部分合成长为$(30 - 2x)$米，宽为$(20 - x)$米的长方形。
根据长方形面积公式可得：$(30 - 2x)(20 - x) = 532$。
展开式子得：$600-30x - 40x+2x^{2}=532$。
整理得：$2x^{2}-70x + 68 = 0$，
两边同时除以$2$得：$x^{2}-35x + 34 = 0$。
分解因式得：$(x - 1)(x - 34)=0$。
则$x - 1 = 0$或$x - 34 = 0$，
解得$x_{1}=1$，$x_{2}=34$。
因为$34＞20$，不符合题意，舍去。
所以$x = 1$。
答：小道进出口的宽度应为$1$米。