15. 小兰在求一个多项式减去$x^2 - 3x + 5$时,误认为加上$x^2 - 3x + 5$,得到的答案是$5x^2 - 2x + 4$,则正确的答案是
$3x^{2}+4x-6$
.
答案:
$3x^{2}+4x-6$
16. 下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中只有两个面涂色的小立方体共有
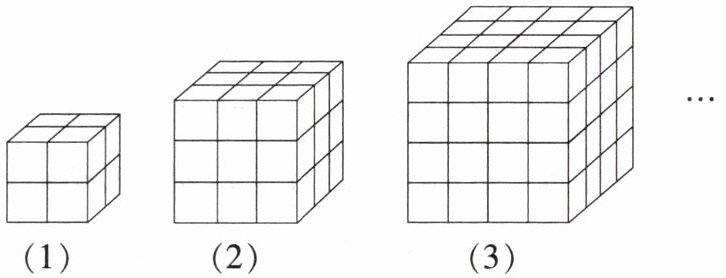
$(8n-4)$
个.
答案:
$(8n-4)$
17. (12分)计算:
(1)$3c^3 - 2c^2 + 8c - 13c^3 + 2c - 2c^2 + 3$;
(2)$8x^2 - 4(2x^2 + 3x - 1)$;
(3)$5x^2 - 2(3y^2 - 5x^2) + (-4y^2 + 7xy)$.
(1)$3c^3 - 2c^2 + 8c - 13c^3 + 2c - 2c^2 + 3$;
(2)$8x^2 - 4(2x^2 + 3x - 1)$;
(3)$5x^2 - 2(3y^2 - 5x^2) + (-4y^2 + 7xy)$.
答案:
1. (1)
解:
对$3c^{3}-2c^{2}+8c - 13c^{3}+2c-2c^{2}+3$进行合并同类项。
对于$c^{3}$的同类项:$3c^{3}-13c^{3}=(3 - 13)c^{3}=-10c^{3}$;
对于$c^{2}$的同类项:$-2c^{2}-2c^{2}=(-2-2)c^{2}=-4c^{2}$;
对于$c$的同类项:$8c + 2c=(8 + 2)c = 10c$;
常数项为$3$。
所以$3c^{3}-2c^{2}+8c - 13c^{3}+2c-2c^{2}+3=-10c^{3}-4c^{2}+10c + 3$。
2. (2)
解:
先去括号:$8x^{2}-4(2x^{2}+3x - 1)=8x^{2}-(4×2x^{2}+4×3x-4×1)$。
根据乘法分配律$a(b + c+d)=ab+ac + ad$,这里$a = 4$,$b = 2x^{2}$,$c = 3x$,$d=-1$,则$8x^{2}-(8x^{2}+12x - 4)$。
再去括号得$8x^{2}-8x^{2}-12x + 4$。
然后合并同类项:$(8x^{2}-8x^{2})-12x + 4=-12x + 4$。
3. (3)
解:
先去括号:$5x^{2}-2(3y^{2}-5x^{2})+(-4y^{2}+7xy)=5x^{2}-(2×3y^{2}-2×5x^{2})-4y^{2}+7xy$。
根据乘法分配律$a(b - c)=ab-ac$(这里$a = 2$,$b = 3y^{2}$,$c = 5x^{2}$),得到$5x^{2}-6y^{2}+10x^{2}-4y^{2}+7xy$。
再合并同类项:
对于$x^{2}$的同类项:$5x^{2}+10x^{2}=(5 + 10)x^{2}=15x^{2}$;
对于$y^{2}$的同类项:$-6y^{2}-4y^{2}=(-6-4)y^{2}=-10y^{2}$;
还有$7xy$。
所以$5x^{2}-2(3y^{2}-5x^{2})+(-4y^{2}+7xy)=15x^{2}-10y^{2}+7xy$。
综上,(1)的结果是$-10c^{3}-4c^{2}+10c + 3$;(2)的结果是$-12x + 4$;(3)的结果是$15x^{2}-10y^{2}+7xy$。
解:
对$3c^{3}-2c^{2}+8c - 13c^{3}+2c-2c^{2}+3$进行合并同类项。
对于$c^{3}$的同类项:$3c^{3}-13c^{3}=(3 - 13)c^{3}=-10c^{3}$;
对于$c^{2}$的同类项:$-2c^{2}-2c^{2}=(-2-2)c^{2}=-4c^{2}$;
对于$c$的同类项:$8c + 2c=(8 + 2)c = 10c$;
常数项为$3$。
所以$3c^{3}-2c^{2}+8c - 13c^{3}+2c-2c^{2}+3=-10c^{3}-4c^{2}+10c + 3$。
2. (2)
解:
先去括号:$8x^{2}-4(2x^{2}+3x - 1)=8x^{2}-(4×2x^{2}+4×3x-4×1)$。
根据乘法分配律$a(b + c+d)=ab+ac + ad$,这里$a = 4$,$b = 2x^{2}$,$c = 3x$,$d=-1$,则$8x^{2}-(8x^{2}+12x - 4)$。
再去括号得$8x^{2}-8x^{2}-12x + 4$。
然后合并同类项:$(8x^{2}-8x^{2})-12x + 4=-12x + 4$。
3. (3)
解:
先去括号:$5x^{2}-2(3y^{2}-5x^{2})+(-4y^{2}+7xy)=5x^{2}-(2×3y^{2}-2×5x^{2})-4y^{2}+7xy$。
根据乘法分配律$a(b - c)=ab-ac$(这里$a = 2$,$b = 3y^{2}$,$c = 5x^{2}$),得到$5x^{2}-6y^{2}+10x^{2}-4y^{2}+7xy$。
再合并同类项:
对于$x^{2}$的同类项:$5x^{2}+10x^{2}=(5 + 10)x^{2}=15x^{2}$;
对于$y^{2}$的同类项:$-6y^{2}-4y^{2}=(-6-4)y^{2}=-10y^{2}$;
还有$7xy$。
所以$5x^{2}-2(3y^{2}-5x^{2})+(-4y^{2}+7xy)=15x^{2}-10y^{2}+7xy$。
综上,(1)的结果是$-10c^{3}-4c^{2}+10c + 3$;(2)的结果是$-12x + 4$;(3)的结果是$15x^{2}-10y^{2}+7xy$。
18. (12分)先化简,再求值:
(1)$(3a^2 - ab + 7) - (5ab - 4a^2 + 7)$,其中,$a = 2,b = \frac{1}{3}$;
(2)$3(ab - 5b^2 + 2a^2) - (7ab + 16a^2 - 25b^2)$,其中$|a - 1| + (b + 1)^2 = 0$.
(1)$(3a^2 - ab + 7) - (5ab - 4a^2 + 7)$,其中,$a = 2,b = \frac{1}{3}$;
(2)$3(ab - 5b^2 + 2a^2) - (7ab + 16a^2 - 25b^2)$,其中$|a - 1| + (b + 1)^2 = 0$.
答案:
(1)解:原式$=3a^{2}-ab+7-5ab+4a^{2}-7$$=7a^{2}-6ab$.
当$a=2,b=\frac{1}{3}$时代入
原式$=7×2^{2}-6×2×\frac{1}{3}$$=24$.
(2)解:原式$=3ab-15b^{2}+6a^{2}-7ab-16a^{2}+25b^{2}$$=-10a^{2}-4ab+10b^{2}$.
因为$|a-1|+(b+1)^{2}=0$,
所以$a-1=0,b+1=0$,即$a=1,b=-1$.
当$a=1,b=-1$时代入
原式$=-10×1^{2}-4×1×(-1)+10×(-1)^{2}=4$.
(1)解:原式$=3a^{2}-ab+7-5ab+4a^{2}-7$$=7a^{2}-6ab$.
当$a=2,b=\frac{1}{3}$时代入
原式$=7×2^{2}-6×2×\frac{1}{3}$$=24$.
(2)解:原式$=3ab-15b^{2}+6a^{2}-7ab-16a^{2}+25b^{2}$$=-10a^{2}-4ab+10b^{2}$.
因为$|a-1|+(b+1)^{2}=0$,
所以$a-1=0,b+1=0$,即$a=1,b=-1$.
当$a=1,b=-1$时代入
原式$=-10×1^{2}-4×1×(-1)+10×(-1)^{2}=4$.
19. (9分)小强和小亮在同时计算这样一道求值题:“当$a = -3$时,求整式$7a^2 - [5a - (4a - 1) + 4a^2] - (2a^2 - a + 1)$的值.”小亮求得正确结果为7,而小强在计算时,错把$a = -3看成了a = 3$,但计算的结果却也正确,你能说明为什么吗?
答案:
解:化简后的结果是$a^{2}-2$,只要a的取值互为相反数,计算结果总是相等的.
查看更多完整答案,请扫码查看


