《2025年新课程能力培养八年级数学上册人教版》

1. 如图，河道 $ m $ 的同侧有 $ M $，$ N $ 两个村庄，计划铺设一条管道将河水引至 $ M $，$ N $ 两村，下面的四个方案中，管道长度最短的是（C）

答案： 1.C　

2. 如图，在四边形 $ ABCD $ 中，$ \angle BAD = 130^{\circ} $，$ \angle B = \angle D = 90^{\circ} $，点 $ E $，$ F $ 分别是线段 $ BC $，$ DC $ 上的动点. 当 $ \triangle AEF $ 的周长最小时，$ \angle EAF $ 的度数为（ ）

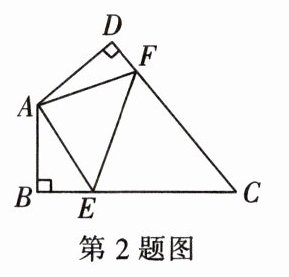
答案： 2.B

3. 如图，要在一条笔直的路边 $ l $ 上建一个燃气站，向 $ l $ 同侧的 $ A $，$ B $ 两个城镇分别铺设管道输送燃气. 试确定燃气站的位置，使铺设管道的路线最短.

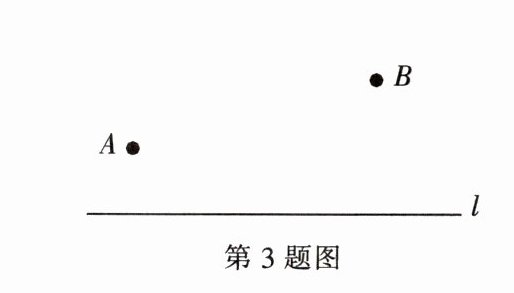
答案：
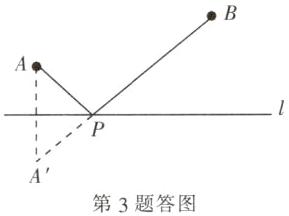
3.解:如图，点P即为所求. 沿AP—PB路线铺设管道，管道长度最短.

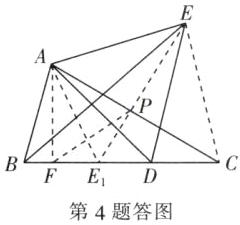
4. 如图，在等腰 $ \triangle ABC $ 中，$ \angle ACB = 30^{\circ} $，$ AC = BC $，点 $ D $ 为直线 $ BC $ 上一点，以 $ AD $ 为边作等边三角形 $ ADE $，连接 $ BE $，当 $ AE + BE $ 取最小值时，求 $ \angle BAE $ 的度数.

答案：
4.解:如图，过点A作AF⊥BC于点F，过点E作EP⊥AC于点P，连接FP，
∵∠ACB=30°，
∴∠FAC=60°.在等边三角形ADE中，∠DAE=60°=∠FAC，AD=AE，
∴∠DAE - ∠DAC=∠FAC - ∠DAC，即∠FAD=∠PAE.在△FAD和△PAE中，∠AFD=∠APE=90°，∠FAD=∠PAE，AD=AE，
∴△FAD≌△PAE（AAS），
∴AF=AP，
∵∠FAC=60°，
∴∠AFP=60°，AP=PF，
∵点D为直线BC上一点，
∴点E在直线EP上运动，
∵∠PFC=∠AFC - ∠AFP=30°=∠ACB，
∴PF=PC=AP，即点P为AC的中点，连接CE，即AE=CE，
∴AE+BE=BE+CE＞BC.当点B，E，C共线时，即点E为图中的点E₁，
∴AE+BE=AE₁+BE₁=BC为AE+BE的最小值，连接AE₁，则∠E₁AC=∠ACB=30°.
∵AB=AC，
∴∠BAC=$\frac{180° - 30°}{2}$=75°，
∴∠BAE₁=∠BAC - ∠E₁AC=45°，
∴当AE+BE取最小值时，∠BAE的度数为45°.

5. 作图题.
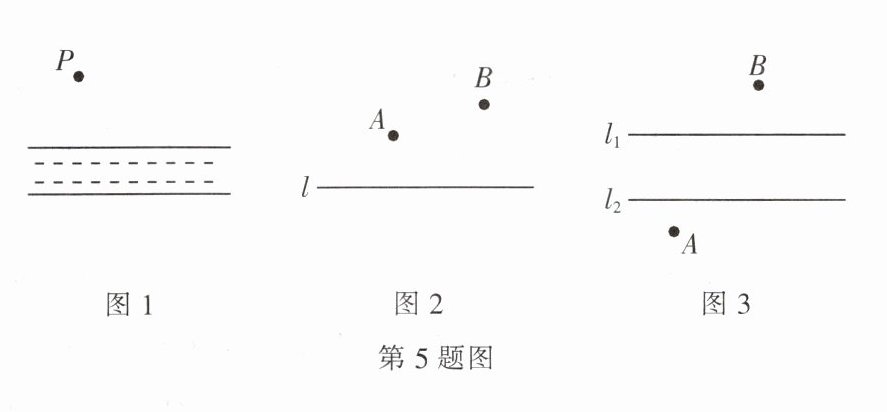
（1）如图 1，一个牧童从 $ P $ 点出发，赶着羊群去河边喝水，则应当怎样选择饮水路线，才能使羊群走的路程最短？请在图中画出最短路线.
（2）如图 2，直线 $ l $ 是一条河，$ A $，$ B $ 是两个村庄，欲在 $ l $ 上的某处修建一个水泵站 $ M $，向 $ A $，$ B $ 两村供水，要使所需管道 $ MA + MB $ 的长度最短，在图中标出 $ M $ 点.
（3）如图 3，在一条河的两岸有 $ A $，$ B $ 两个村庄，现在要在河上建一座小桥，桥的方向与河岸方向垂直，桥在图中用一条线段 $ CD $ 表示. 试问：桥 $ CD $ 建在何处，才能使 $ A $ 到 $ B $ 的路程最短？请在图中画出桥 $ CD $ 的位置. 画出示意图，并用平移的原理说明理由.

答案：
5.解:（1）如图1.（2）如图2.

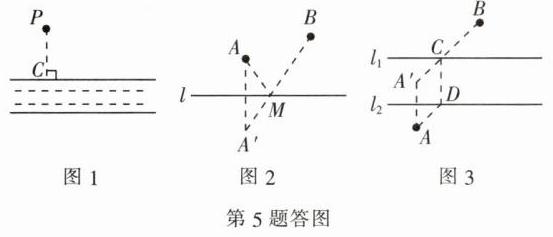
（3）如图3，先确定AA'=CD，且AA'//CD，连接BA'，与河岸的交点就是点C，过点C作CD垂直河岸，交另一河岸于点D，CD就是所求的桥的位置. 理由:由作图过程可知，四边形ADCA'为平行四边形，AD平移至A'C即可得到线段A'B，两点之间，线段最短，由于河宽不变，CD即为桥.

6. (2023·白塔) 在一条沿直线 $ MN $ 铺设的电缆两侧有甲、乙两个小区，现要求在 $ MN $ 上选取一点 $ P $，向两个小区铺设电缆. 下面四种铺设方案中，使用电缆材料最少的是（ ）

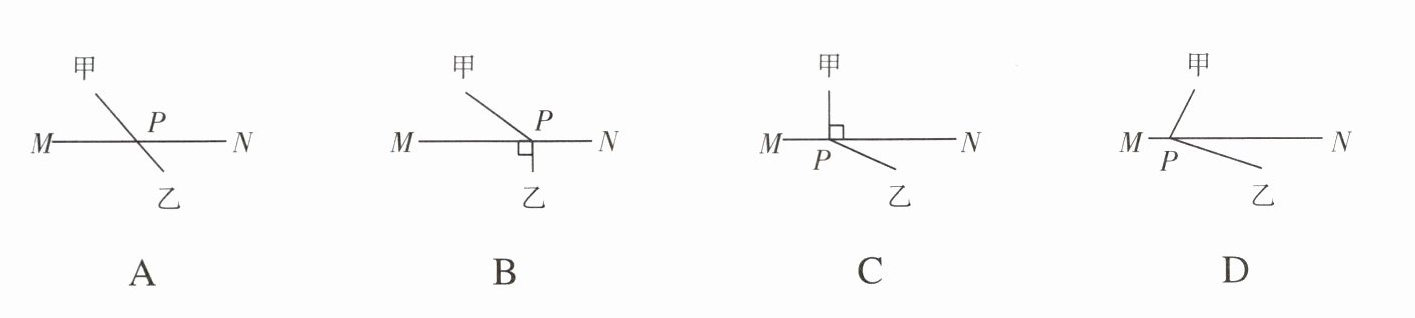
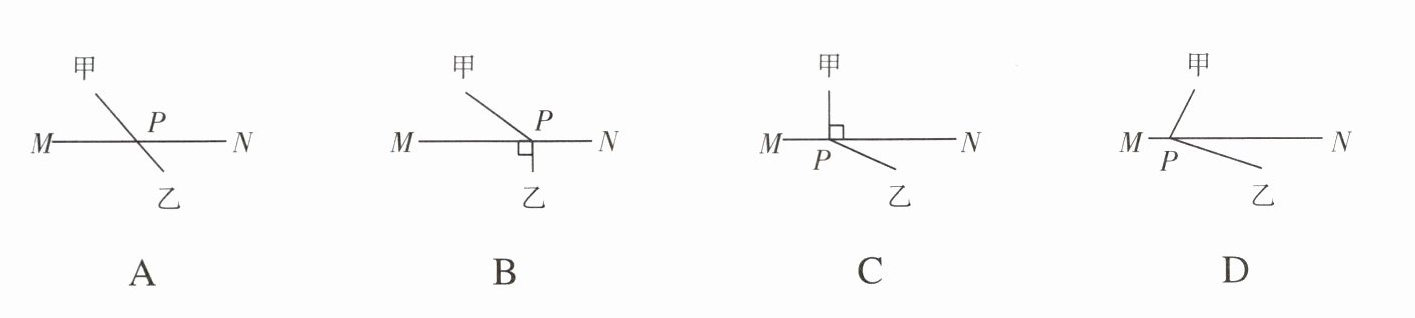
答案： 6.A　

7. (2020·江阴) 如图，已知等边三角形 $ ABC $ 的边长为 $ 4 $，$ P $，$ Q $，$ R $ 分别为边 $ AB $，$ BC $，$ AC $ 上的动点，则 $ PR + QR $ 的最小值是（ ）

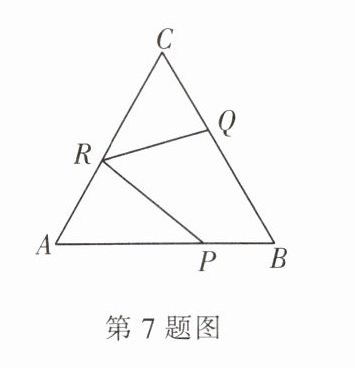
A.$ 2\sqrt{2} $
B.$ 2 $
C.$ 2\sqrt{3} $
D.$ 3\sqrt{2} $

答案： 7.C　

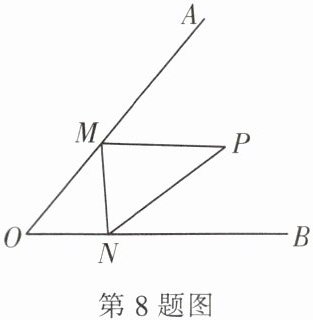
8. (2024·绥化) 如图，已知 $ \angle AOB = 50^{\circ} $，点 $ P $ 为 $ \angle AOB $ 内部一点，点 $ M $ 为射线 $ OA $、点 $ N $ 为射线 $ OB $ 上的两个动点，当 $ \triangle PMN $ 的周长最小时，则 $ \angle MPN = $______.

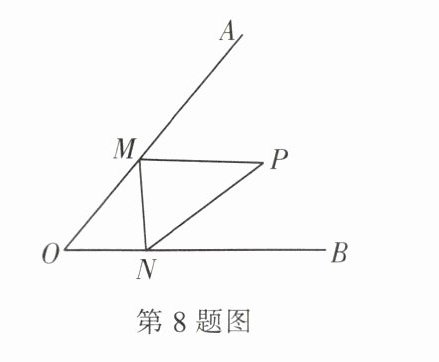
答案： 8.80°