《2025年学习与评价江苏凤凰教育出版社八年级数学上册苏科版》

(1) 在Rt△ABC中，∠ACB=90°，AC=m，BC=n，已知图3-2①中大正方形的面积为61，小正方形的面积为1，求(m+n)²；
(2) 若将图3-2①中的四个直角三角形中较长的直角边分别向外延长一倍，得到图3-2②所示的“数学风车”，这个风车的外围周长（图中实线部分）为40.

答案：
(1) 解：
∵大正方形面积为61，小正方形面积为1，
∴四个直角三角形面积和为61-1=60，
每个直角三角形面积为$\frac{1}{2}mn=15$，即$mn=30$。
由勾股定理得$m^2+n^2=61$，
$\therefore (m+n)^2=m^2+n^2+2mn=61+60=121$。
(2) 40

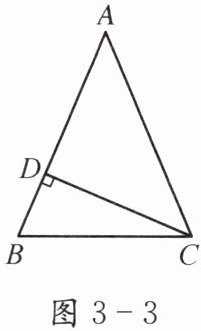
例1 如图3-3，在△ABC中，AB=AC=13，BC=10，CD⊥BC，垂足为D.求高CD的长.

答案： 解：过点A作AE⊥BC于点E，
∵AB=AC=13，BC=10，
∴BE=EC=5（等腰三角形三线合一），
在Rt△AEC中，AE² + EC² = AC²，
即AE² + 5² = 13²，
解得AE=12，
S△ABC = 1/2×BC×AE = 1/2×10×12 = 60，
又
∵S△ABC = 1/2×AB×CD，
∴1/2×13×CD = 60，
解得CD=120/13.

例2 请用勾股定理证明“斜边和一条直角边对应相等的两个直角三角形全等”.

答案： 【解析】：
本题主要考查勾股定理和直角三角形全等的判定。
首先，我们设定两个直角三角形，它们的斜边和一条直角边分别相等。
设两个直角三角形分别为$\triangle ABC$和$\triangle A'B'C'$，其中$\angle B$和$\angle B'$为直角，$AB = A'B'$为斜边，$AC = A'C'$为一条直角边。
根据勾股定理，对于直角三角形，其两直角边的平方和等于斜边的平方。
因此，在$\triangle ABC$中，有$BC^2 = AB^2 - AC^2$；
在$\triangle A'B'C'$中，有$B'C'^2 = A'B'^2 - A'C'^2$。
由于$AB = A'B'$且$AC = A'C'$，代入上述公式可得$BC^2 = B'C'^2$，进一步开方得到$BC = B'C'$。
至此，我们证明了两个直角三角形的三边分别相等，即$AB = A'B'$，$AC = A'C'$，$BC = B'C'$。
根据三边全等的判定定理(SSS)，我们可以得出$\triangle ABC \cong \triangle A'B'C'$。
【答案】：
证明：
设两个直角三角形分别为$\triangle ABC$和$\triangle A'B'C'$，其中$\angle B$，$\angle B'$为直角，且$AB = A'B'$，$AC = A'C'$。
∵根据勾股定理，在直角三角形中，直角边的平方和等于斜边的平方，
∴$BC^2 = AB^2 - AC^2$，$B'C'^2 = A'B'^2 - A'C'^2$，
∵$AB = A'B'$且$AC = A'C'$，
∴$BC^2 = B'C'^2$，
进一步开方，得$BC = B'C'$，
在$\triangle ABC$和$\triangle A'B'C'$中，
∵$AB = A'B'$，$AC = A'C'$，$BC = B'C'$，
∴根据三边全等的判定定理(SSS)，$\triangle ABC \cong \triangle A'B'C'$。