《2025年学习与评价江苏凤凰教育出版社八年级数学上册苏科版》

4. 把下列各数填入相应的横线上：
$0$,$-7.5$,$\sqrt{\frac{9}{14}}$,$(\sqrt[3]{5}-\sqrt{2})^0$,$4.\dot{2}\dot{1}$,$3.14159$,$-\left|-\frac{3}{4}\right|$,$20\%$,$\sqrt[3]{-8}$
(1)有理数：$0$，$-7.5$，$(\sqrt[3]{5}-\sqrt{2})^0$，$4.\dot{2}\dot{1}$，$3.14159$，$-\left|-\frac{3}{4}\right|$，$20\%$，$\sqrt[3]{-8}$；
(2)无理数：$\sqrt{\frac{9}{14}}$；
(3)正实数：$\sqrt{\frac{9}{14}}$，$(\sqrt[3]{5}-\sqrt{2})^0$，$4.\dot{2}\dot{1}$，$3.14159$，$20\%$；
(4)负实数：$-7.5$，$-\left|-\frac{3}{4}\right|$，$\sqrt[3]{-8}$.

答案： 【解析】：
本题主要考察实数的分类，包括有理数、无理数、正实数和负实数的识别。
(1)有理数是可以表示为两个整数的比的数，包括整数、有限小数和循环小数。
(2)无理数则不能表示为两个整数的比，常见的无理数有开方后不是整数的数值、π、e等。
(3)正实数是大于0的实数。
(4)负实数是小于0的实数。
接下来，我们逐一判断给出的数：
$0$：是有理数，也是实数，但不是正实数也不是负实数。
$-7.5$：是有理数，也是负实数。
$\sqrt{\frac{9}{14}}$：是无理数，因为开方后不能得到整数或有限小数，同时也是正实数。
$(\sqrt[3]{5}-\sqrt{2})^0$：任何非零数的0次方都是1，所以这是有理数，也是正实数。
$4.\dot{2}\dot{1}$：是循环小数，所以是有理数，也是正实数。
$3.14159$：是有限小数，所以是有理数，也是正实数。
$-\left|-\frac{3}{4}\right|$：计算得$-\frac{3}{4}$，是有理数，也是负实数。
$20\%$：等于0.2，是有理数，也是正实数。
$\sqrt[3]{-8}$：计算得-2，是有理数，也是负实数。
【答案】：
(1)有理数：$0$，$-7.5$，$(\sqrt[3]{5}-\sqrt{2})^0$，$4.\dot{2}\dot{1}$，$3.14159$，$-\left|-\frac{3}{4}\right|$，$20\%$，$\sqrt[3]{-8}$；
(2)无理数：$\sqrt{\frac{9}{14}}$；
(3)正实数：$\sqrt{\frac{9}{14}}$，$(\sqrt[3]{5}-\sqrt{2})^0$，$4.\dot{2}\dot{1}$，$3.14159$，$20\%$；
(4)负实数：$-7.5$，$-\left|-\frac{3}{4}\right|$，$\sqrt[3]{-8}$。

5. (1)如图,数轴上的点A,B表示的数分别是什么？

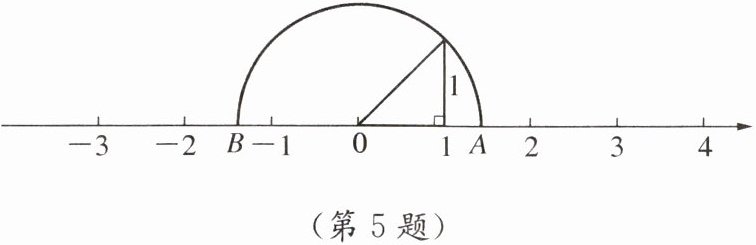
(2)在数轴上表示出$\sqrt{3}和\sqrt{5}$的大概位置,并分别找到一个有理数a和无理数b,使得$\sqrt{3}＜a＜\sqrt{5}$,$\sqrt{3}＜b＜\sqrt{5}$.

答案：
$(1)$解：点$A$表示的数是$\sqrt 2，$点$B$表示的数是$-\sqrt 2。$$ $　　
$(2)$解：在数轴上，$√3$位于$1$和$2$之间靠近$2$的位置，$√5$位于$2$和$3$之间靠近$2$的位置$（$画图略$）。$$a=2（$答案不唯一$），$$b=√3+0.1（$答案不唯一$）。$$ $　　

6. 在数轴上,点A,B表示的数分别是$1$,$\sqrt{5}$,点C在点A左侧,且$AC= AB$,求点C表示的数.

答案： 解：
∵点A，B表示的数分别是1，$\sqrt{5}$，
∴AB=$\sqrt{5}-1$。
∵AC=AB，
∴AC=$\sqrt{5}-1$。
∵点C在点A左侧，
∴点C表示的数为$1-(\sqrt{5}-1)=2-\sqrt{5}$。
答：点C表示的数为$2-\sqrt{5}$。