《2025年学习与评价江苏凤凰教育出版社八年级数学上册苏科版》

画△ABC,使∠A= 30°,AB= 3 cm,BC= 2 cm.你画的三角形与其他同学画的三角形全等吗？

答案： 解：
1. 画∠MAN=30°；
2. 在射线AM上截取AB=3cm；
3. 以点B为圆心，2cm为半径画弧，交射线AN于点C₁、C₂；
4. 连接BC₁、BC₂，得到△ABC₁和△ABC₂。
结论：所画三角形与其他同学画的三角形不一定全等。

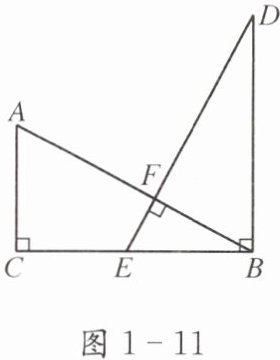
例 如图1-11,AC⊥CB,DB⊥CB,AB⊥DE,垂足分别为C,B,F,AB= DE,E是BC的中点.
(1)观察并猜想BD与BC有何数量关系,并证明你的猜想；
(2)已知BD= 6,求AC的长.

答案：
(1)猜想：BD=BC。
证明：
∵AC⊥CB，DB⊥CB，AB⊥DE，
∴∠C=∠DBE=∠DFB=90°，
∴∠A+∠ABC=90°，∠DEB+∠ABC=90°，
∴∠A=∠DEB。
在△ACB和△EBD中，
∵∠C=∠DBE，∠A=∠DEB，AB=DE，
∴△ACB≌△EBD(AAS)，
∴BD=BC。
(2)
∵△ACB≌△EBD，
∴AC=EB。
∵E是BC的中点，BD=BC=6，
∴EB=BC/2=3，
∴AC=3。

1. 判断题(正确的打“√”,错误的打“×”)：
(1)有三个角相等的两个三角形全等；(×)
(2)面积相等的两个三角形全等；(×)
(3)有两边及其中一边所对的角分别相等的两个三角形全等；(×)
(4)有一个锐角相等且有一条直角边相等的两个直角三角形全等.(√)

答案： 【解析】：
本题主要考察全等三角形的判定条件。
(1) 有三个角相等的两个三角形只能说明它们相似，但不能说明它们全等。因为全等三角形除了角度相等外，还需要边长相等。所以此命题是错误的。
(2) 面积相等的两个三角形不一定全等。例如，高和底相同但形状不同的两个三角形可能有相同的面积，但它们的边长和角度可能并不完全相等。所以此命题是错误的。
(3) 有两边及其中一边所对的角分别相等的两个三角形，这实际上是SSA的情况，但SSA并不是全等三角形的一个判定条件。所以此命题是错误的。
(4) 有一个锐角相等且有一条直角边相等的两个直角三角形，这实际上是ASA或AAS的情况（因为直角三角形已经隐含了一个90度的角），所以这两个三角形是全等的。但此命题的表述可能产生歧义，因为它没有明确另一条边或另一个角是否相等，但按照常规理解，当一个锐角和一条直角边相等时，且都是直角三角形，我们可以认为它们满足ASA或AAS的条件，因此此命题在本题的语境下是正确的，但严格来说，它不如直接表述为“有一个锐角和两条边分别相等的两个直角三角形全等”来得准确。但按照题目的原意，我们判断此命题为正确，但在数学严谨性上略有欠缺。不过按照题目的要求，我们主要考察的是学生对全等三角形判定条件的理解，所以此命题判断为正确。
【答案】：
(1) ×
(2) ×
(3) ×
(4) √

2. (1)如图,已知AD= AB,∠C= ∠E,∠CDE= 55°,则∠ABE= ______°；

125
(2)如图,点D,E,F,B在一条直线上,AB//CD,AE//CF,且AE= CF,已知BD= 10,BF= 2,则EF= ______.

6

答案：
(1)证明：
∵∠CDE=55°，∠CDE+∠ADE=180°，
∴∠ADE=125°.
在△ADE和△ABC中，
∠C=∠E，∠A=∠A，AD=AB，
∴△ADE≌△ABC(AAS)，
∴∠ABE=∠ADE=125°.
故答案为：125.
(2)证明：
∵AB//CD，AE//CF，
∴∠B=∠D，∠AEB=∠CFD.
在△ABE和△CDF中，
∠B=∠D，∠AEB=∠CFD，AE=CF，
∴△ABE≌△CDF(AAS)，
∴BE=DF.
∵BD=10，BF=2，
∴DF=BD-BF=8，
∴BE=8，
∴EF=BE-BF=6.
故答案为：6.