1. 下列长度的三条线段不能组成三角形的是(
A.3,4,7
B.3,4,6
C.3,4,5
D.3,4,4
A
).A.3,4,7
B.3,4,6
C.3,4,5
D.3,4,4
答案:
解:根据三角形三边关系,任意两边之和大于第三边。
A. $3 + 4 = 7$,不满足两边之和大于第三边,不能组成三角形;
B. $3 + 4 > 6$,$3 + 6 > 4$,$4 + 6 > 3$,能组成三角形;
C. $3 + 4 > 5$,$3 + 5 > 4$,$4 + 5 > 3$,能组成三角形;
D. $3 + 4 > 4$,$3 + 4 > 4$,$4 + 4 > 3$,能组成三角形。
结论:A
A. $3 + 4 = 7$,不满足两边之和大于第三边,不能组成三角形;
B. $3 + 4 > 6$,$3 + 6 > 4$,$4 + 6 > 3$,能组成三角形;
C. $3 + 4 > 5$,$3 + 5 > 4$,$4 + 5 > 3$,能组成三角形;
D. $3 + 4 > 4$,$3 + 4 > 4$,$4 + 4 > 3$,能组成三角形。
结论:A
2. 如图,AB= AC,AD= AE,为使△ABD≌△ACE,可以补充的条件是(
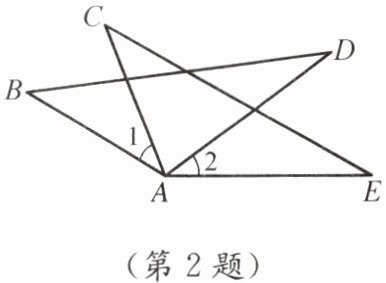
A.∠B= ∠C
B.∠D= ∠E
C.∠1= ∠2
D.∠CAD= ∠DAC
C
).
A.∠B= ∠C
B.∠D= ∠E
C.∠1= ∠2
D.∠CAD= ∠DAC
答案:
【解析】:本题考查全等三角形的判定定理。
题目给出了两个三角形$\bigtriangleup ABD$和$\bigtriangleup ACE$,其中$AB = AC$,$AD = AE$,需要找到一个条件使得这两个三角形全等。
A选项:$\angle B = \angle C$。
这个条件给出了两个三角形的两组对应边相等,但给出的角并不是这两组对应边的夹角,所以不能根据$SAS$(边角边)判定三角形全等。
同时,没有给出足够的信息来应用其他全等判定定理(如$SSS$,$ASA$,$AAS$等),因此A选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
B选项:$\angle D = \angle E$。
与A选项类似,这个条件给出了两个三角形的两组对应边相等,但给出的角并不是对应边的夹角,所以不能根据$SAS$判定三角形全等。
同样,没有足够的信息来应用其他全等判定定理,因此B选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
C选项:$\angle 1 = \angle 2$。
由于$\angle BAD = \angle 1 + \angle CAD$,$\angle CAE = \angle 2 + \angle CAD$,且$\angle 1 = \angle 2$,
所以$\angle BAD = \angle CAE$。
现在,我们有了两组对应边相等($AB = AC$,$AD = AE$)和它们之间的夹角相等($\angle BAD = \angle CAE$),这满足$SAS$(边角边)判定定理。
因此,C选项可以使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
D选项:$\angle CAD = \angle DAC$。
这个条件实际上是一个自明的事实,因为任何角都等于它自身。
它并没有提供任何新的信息来帮助我们判定两个三角形是否全等。
因此,D选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
综上所述,只有C选项可以使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
【答案】:C。
题目给出了两个三角形$\bigtriangleup ABD$和$\bigtriangleup ACE$,其中$AB = AC$,$AD = AE$,需要找到一个条件使得这两个三角形全等。
A选项:$\angle B = \angle C$。
这个条件给出了两个三角形的两组对应边相等,但给出的角并不是这两组对应边的夹角,所以不能根据$SAS$(边角边)判定三角形全等。
同时,没有给出足够的信息来应用其他全等判定定理(如$SSS$,$ASA$,$AAS$等),因此A选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
B选项:$\angle D = \angle E$。
与A选项类似,这个条件给出了两个三角形的两组对应边相等,但给出的角并不是对应边的夹角,所以不能根据$SAS$判定三角形全等。
同样,没有足够的信息来应用其他全等判定定理,因此B选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
C选项:$\angle 1 = \angle 2$。
由于$\angle BAD = \angle 1 + \angle CAD$,$\angle CAE = \angle 2 + \angle CAD$,且$\angle 1 = \angle 2$,
所以$\angle BAD = \angle CAE$。
现在,我们有了两组对应边相等($AB = AC$,$AD = AE$)和它们之间的夹角相等($\angle BAD = \angle CAE$),这满足$SAS$(边角边)判定定理。
因此,C选项可以使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
D选项:$\angle CAD = \angle DAC$。
这个条件实际上是一个自明的事实,因为任何角都等于它自身。
它并没有提供任何新的信息来帮助我们判定两个三角形是否全等。
因此,D选项不能使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
综上所述,只有C选项可以使$\bigtriangleup ABD \cong \bigtriangleup ACE$。
【答案】:C。
3. 如图,AC= AD,BC= BD,则有(

A.AB⊥CD,OC= OD
B.AB⊥CD,OA= OB
C.AB⊥CD,OA= OB,OC= OD
D.CD平分∠ACB
A
).
A.AB⊥CD,OC= OD
B.AB⊥CD,OA= OB
C.AB⊥CD,OA= OB,OC= OD
D.CD平分∠ACB
答案:
解:在△ACB和△ADB中,
∵AC=AD,BC=BD,AB=AB,
∴△ACB≌△ADB(SSS),
∴∠CAB=∠DAB,
在△ACO和△ADO中,
∵AC=AD,∠CAO=∠DAO,AO=AO,
∴△ACO≌△ADO(SAS),
∴OC=OD,∠AOC=∠AOD,
∵∠AOC+∠AOD=180°,
∴∠AOC=∠AOD=90°,
∴AB⊥CD,OC=OD。
答案:A
∵AC=AD,BC=BD,AB=AB,
∴△ACB≌△ADB(SSS),
∴∠CAB=∠DAB,
在△ACO和△ADO中,
∵AC=AD,∠CAO=∠DAO,AO=AO,
∴△ACO≌△ADO(SAS),
∴OC=OD,∠AOC=∠AOD,
∵∠AOC+∠AOD=180°,
∴∠AOC=∠AOD=90°,
∴AB⊥CD,OC=OD。
答案:A
4. 如图,下列条件中,不能说明△ABD≌△ACD的是(

A.BD= CD,AB= AC
B.∠ADB= ∠ADC
C.∠B= ∠C,∠BAD= ∠CAD
D.∠B= ∠C,∠ADB= ∠ADC
B
).
A.BD= CD,AB= AC
B.∠ADB= ∠ADC
C.∠B= ∠C,∠BAD= ∠CAD
D.∠B= ∠C,∠ADB= ∠ADC
答案:
【解析】:
本题考查全等三角形的判定定理。
A选项给出了两条边分别相等,即$BD = CD$和$AB = AC$,再加上两个三角形共有的边$AD = AD$,构成了$SSS$(边边边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
B选项只给出了$\angle ADB=\angle ADC$,仅有一个角相等,不满足全等三角形的判定定理,无法判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
C选项给出了两对角分别相等,即$\angle B=\angle C$和$\angle BAD = \angle CAD$,再加上两个三角形共有的边$AD = AD$,构成了$AAS$(角角边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
D选项给出了两对角分别相等,即$\angle B=\angle C$和$\angle ADB=\angle ADC$,再加上两个三角形共有的边$AD = AD$,构成了$AAS$(角角边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
【答案】:B
本题考查全等三角形的判定定理。
A选项给出了两条边分别相等,即$BD = CD$和$AB = AC$,再加上两个三角形共有的边$AD = AD$,构成了$SSS$(边边边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
B选项只给出了$\angle ADB=\angle ADC$,仅有一个角相等,不满足全等三角形的判定定理,无法判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
C选项给出了两对角分别相等,即$\angle B=\angle C$和$\angle BAD = \angle CAD$,再加上两个三角形共有的边$AD = AD$,构成了$AAS$(角角边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
D选项给出了两对角分别相等,即$\angle B=\angle C$和$\angle ADB=\angle ADC$,再加上两个三角形共有的边$AD = AD$,构成了$AAS$(角角边)全等条件,所以可以判定$\bigtriangleup ABD\cong \bigtriangleup ACD$。
【答案】:B
5. 等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角的度数为(
A.40°
B.50°
C.40°或140°
D.50°或130°
D
).A.40°
B.50°
C.40°或140°
D.50°或130°
答案:
【解析】:
本题主要考察等腰三角形的性质以及三角形内角和定理的应用。
首先,我们设等腰三角形为$\triangle ABC$,其中$AB = AC$,且$BD$是$AC$上的高。
当等腰三角形为锐角三角形时:
由题意知,$\angle ABD = 40^\circ$(高与腰的夹角)。
那么,在直角三角形$\triangle ABD$中,有$\angle BAC = 90^\circ - \angle ABD = 90^\circ - 40^\circ = 50^\circ$。
由于$\triangle ABC$是等腰三角形,所以顶角$\angle BAC$就是我们要求的顶角度数,即$50^\circ$。
当等腰三角形为钝角三角形时:
此时,高$BD$在三角形外部。
由题意知,$\angle ABD = 40^\circ$。
在直角三角形$\triangle ABD$中,外角$\angle BAD = 90^\circ - \angle ABD = 90^\circ - 40^\circ = 50^\circ$。
由于$\angle BAD$是三角形的一个外角,根据外角等于两不相邻内角之和,有$\angle BAC = 180^\circ - \angle BAD = 180^\circ - 50^\circ = 130^\circ$。
综合两种情况,等腰三角形的顶角度数可以是$50^\circ$或$130^\circ$。
【答案】:
D. $50^\circ$或$130^\circ$。
本题主要考察等腰三角形的性质以及三角形内角和定理的应用。
首先,我们设等腰三角形为$\triangle ABC$,其中$AB = AC$,且$BD$是$AC$上的高。
当等腰三角形为锐角三角形时:
由题意知,$\angle ABD = 40^\circ$(高与腰的夹角)。
那么,在直角三角形$\triangle ABD$中,有$\angle BAC = 90^\circ - \angle ABD = 90^\circ - 40^\circ = 50^\circ$。
由于$\triangle ABC$是等腰三角形,所以顶角$\angle BAC$就是我们要求的顶角度数,即$50^\circ$。
当等腰三角形为钝角三角形时:
此时,高$BD$在三角形外部。
由题意知,$\angle ABD = 40^\circ$。
在直角三角形$\triangle ABD$中,外角$\angle BAD = 90^\circ - \angle ABD = 90^\circ - 40^\circ = 50^\circ$。
由于$\angle BAD$是三角形的一个外角,根据外角等于两不相邻内角之和,有$\angle BAC = 180^\circ - \angle BAD = 180^\circ - 50^\circ = 130^\circ$。
综合两种情况,等腰三角形的顶角度数可以是$50^\circ$或$130^\circ$。
【答案】:
D. $50^\circ$或$130^\circ$。
6. 如图,在△ABC中,AC= BC,∠ACB= 90°,点D,E在边AB上,将△ACD,△BCE分别沿CD,CE翻折,点A,B分别落在点A',B'的位置,再将△A'CD,△B'CE分别沿A'C,B'C翻折,点D与点E恰好重合于点O,则∠A'OB'的度数是(
A.90°
B.120°
C.135°
D.150°
B
).A.90°
B.120°
C.135°
D.150°
答案:
B
查看更多完整答案,请扫码查看


