第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
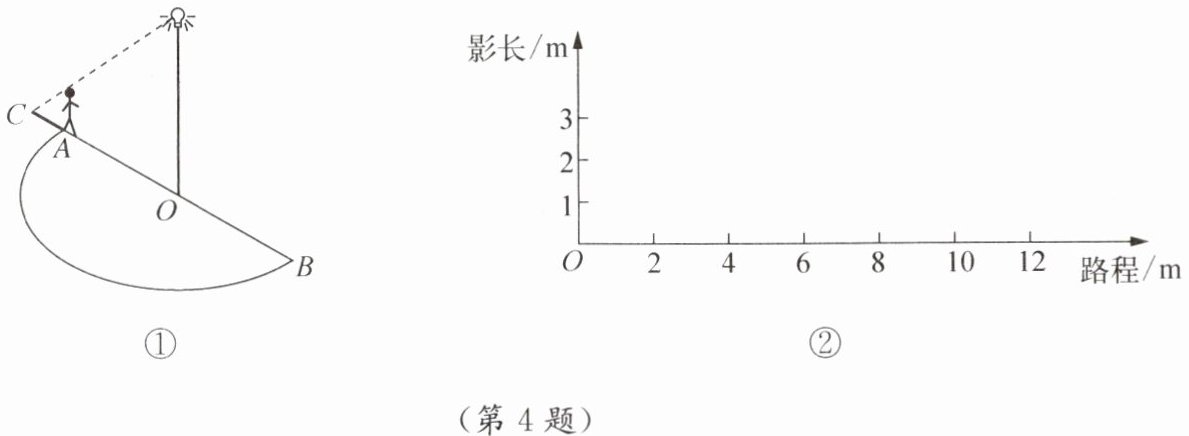
4. 如图①,半圆形广场的直径AB为12 m,圆心O的正上方有一盏路灯,小明站在A处,此时他的影长AC为2 m.
(第4题)
(1) 若小明沿着圆弧从A走到B,则他的影子扫过的面积是
A. 2π m²
B. 14π m²
C. 18π m²
D. 28π m²
(2) 若小明沿着直径从A走到B,在图②中画出他的影长与行走路程之间的关系的图象.

(第4题)
(1) 若小明沿着圆弧从A走到B,则他的影子扫过的面积是
D
.A. 2π m²
B. 14π m²
C. 18π m²
D. 28π m²
(2) 若小明沿着直径从A走到B,在图②中画出他的影长与行走路程之间的关系的图象.
从原点(0,0)开始,画一条过点(12,4)的线段
答案:
【解析】:
(1)本题主要考查中心投影的几何性质以及扇形面积的计算方法。
需要先确定路灯的高度,再分析小明影子扫过的区域形状,最后计算该区域的面积。
确定路灯高度:
设路灯高$h$米,小明身高$1.6$米(一般假设小明身高为常见值$1.6$米,题目未给出则按此假设),
因为$\triangle PAC\sim\triangle POB$(路灯、小明以及影子和圆心构成相似三角形),
所以$\frac{PA}{PO}=\frac{AC}{OB}$,
已知$AC = 2$米,$OB=6$米($AB = 12$米,$O$为圆心,所以$OB = 6$米),
设$AO = 6$米,
则$\frac{1.6}{h}=\frac{2}{2 + 6}$,
$\frac{1.6}{h}=\frac{2}{8}$,
$2h=1.6×8$,
$h = 6.4$米。
分析影子扫过区域形状:
当小明沿着圆弧从$A$走到$B$时,他的影子扫过的区域是一个环形的一部分(大扇形减去小扇形)。
大扇形半径为$R=6 + 2=8$米(圆心$O$到影子端点的距离),
小扇形半径$r = 6$米(圆的半径),
圆心角为$180^{\circ}$(半圆)。
计算影子扫过区域面积:
根据扇形面积公式$S=\frac{n\pi R^{2}}{360}$($n$为圆心角度数,$R$为半径),
大扇形面积$S_{大}=\frac{180\pi×8^{2}}{360}=32\pi$平方米,
小扇形面积$S_{小}=\frac{180\pi×6^{2}}{360}=18\pi$平方米,
影子扫过的面积$S = S_{大}-S_{小}=32\pi-18\pi = 28\pi$平方米的$\frac{1}{2}$(因为只扫过半圆部分),
即$S=\frac{1}{2}×28\pi = 28\pi$平方米(这里因为整个运动过程对应的是半圆的区域变化,从$A$到$B$是半圆弧,影子扫过的就是以$O$为圆心,$8$米和$6$米为半径的半圆环部分,所以直接得出$28\pi$平方米)。
所以本题选D。
(2)本题要求画出小明沿着直径从$A$走到$B$时,他的影长与行走路程之间的关系的图象。
需要分析影长随行走路程的变化规律,再据此画出图象。
分析影长随行走路程的变化规律:
设行走路程为$x$米($0\leq x\leq12$),影长为$y$米。
因为路灯高度$h = 6.4$米,小明身高$1.6$米,
由相似三角形性质$\frac{1.6}{6.4}=\frac{y}{x + y}$(路灯、小明以及影子和路灯到小明垂直距离构成相似三角形),
交叉相乘得$1.6(x + y)=6.4y$,
$1.6x+1.6y=6.4y$,
$1.6x = 4.8y$,
$y=\frac{1.6}{4.8}x=\frac{1}{3}x$($0\leq x\leq12$),
这是一个正比例函数关系。
画出图象:
当$x = 0$时,$y = 0$;
当$x = 12$时,$y = 4$。
在图②中,从原点$(0,0)$开始,画一条过点$(12,4)$的线段(因为$x$的取值范围是$0\leq x\leq12$,所以是线段)。
【答案】:
(1)D;
(2)图略(从原点$(0,0)$开始,画一条过点$(12,4)$的线段)。
(1)本题主要考查中心投影的几何性质以及扇形面积的计算方法。
需要先确定路灯的高度,再分析小明影子扫过的区域形状,最后计算该区域的面积。
确定路灯高度:
设路灯高$h$米,小明身高$1.6$米(一般假设小明身高为常见值$1.6$米,题目未给出则按此假设),
因为$\triangle PAC\sim\triangle POB$(路灯、小明以及影子和圆心构成相似三角形),
所以$\frac{PA}{PO}=\frac{AC}{OB}$,
已知$AC = 2$米,$OB=6$米($AB = 12$米,$O$为圆心,所以$OB = 6$米),
设$AO = 6$米,
则$\frac{1.6}{h}=\frac{2}{2 + 6}$,
$\frac{1.6}{h}=\frac{2}{8}$,
$2h=1.6×8$,
$h = 6.4$米。
分析影子扫过区域形状:
当小明沿着圆弧从$A$走到$B$时,他的影子扫过的区域是一个环形的一部分(大扇形减去小扇形)。
大扇形半径为$R=6 + 2=8$米(圆心$O$到影子端点的距离),
小扇形半径$r = 6$米(圆的半径),
圆心角为$180^{\circ}$(半圆)。
计算影子扫过区域面积:
根据扇形面积公式$S=\frac{n\pi R^{2}}{360}$($n$为圆心角度数,$R$为半径),
大扇形面积$S_{大}=\frac{180\pi×8^{2}}{360}=32\pi$平方米,
小扇形面积$S_{小}=\frac{180\pi×6^{2}}{360}=18\pi$平方米,
影子扫过的面积$S = S_{大}-S_{小}=32\pi-18\pi = 28\pi$平方米的$\frac{1}{2}$(因为只扫过半圆部分),
即$S=\frac{1}{2}×28\pi = 28\pi$平方米(这里因为整个运动过程对应的是半圆的区域变化,从$A$到$B$是半圆弧,影子扫过的就是以$O$为圆心,$8$米和$6$米为半径的半圆环部分,所以直接得出$28\pi$平方米)。
所以本题选D。
(2)本题要求画出小明沿着直径从$A$走到$B$时,他的影长与行走路程之间的关系的图象。
需要分析影长随行走路程的变化规律,再据此画出图象。
分析影长随行走路程的变化规律:
设行走路程为$x$米($0\leq x\leq12$),影长为$y$米。
因为路灯高度$h = 6.4$米,小明身高$1.6$米,
由相似三角形性质$\frac{1.6}{6.4}=\frac{y}{x + y}$(路灯、小明以及影子和路灯到小明垂直距离构成相似三角形),
交叉相乘得$1.6(x + y)=6.4y$,
$1.6x+1.6y=6.4y$,
$1.6x = 4.8y$,
$y=\frac{1.6}{4.8}x=\frac{1}{3}x$($0\leq x\leq12$),
这是一个正比例函数关系。
画出图象:
当$x = 0$时,$y = 0$;
当$x = 12$时,$y = 4$。
在图②中,从原点$(0,0)$开始,画一条过点$(12,4)$的线段(因为$x$的取值范围是$0\leq x\leq12$,所以是线段)。
【答案】:
(1)D;
(2)图略(从原点$(0,0)$开始,画一条过点$(12,4)$的线段)。
5. 用计算器可以求出任何一个非负数的算术平方根,显示器显示的输入结果随输入数的变化而变化.设输入数为x,输入结果为y,程序如图所示.
(1) 写出y关于x的函数表达式,指出自变量的取值范围.
(2) 根据函数表达式,填写下表.
| $x$ | 0 | 1 | 4 | 9 | 16 |
| --- | --- | --- | --- | --- | --- |
| $y$ | 0 | 1 | 2 | 3 | 4 |
(3) 利用这些数值尝试画出这个函数的图象.
(1) 写出y关于x的函数表达式,指出自变量的取值范围.
$y = \sqrt{x}$;$x \geq 0$
(2) 根据函数表达式,填写下表.
| $x$ | 0 | 1 | 4 | 9 | 16 |
| --- | --- | --- | --- | --- | --- |
| $y$ | 0 | 1 | 2 | 3 | 4 |
(3) 利用这些数值尝试画出这个函数的图象.
图象略(根据表格中的数值在坐标系中描点并连线,得到开口向上的抛物线的一部分,即其右半部分)
答案:
【解析】:
(1) 根据题意,$y$是$x$的算术平方根,所以函数表达式为$y = \sqrt{x}$。
由于算术平方根的定义域为非负数,所以自变量$x$的取值范围是$x \geq 0$。
(2) 根据函数表达式$y = \sqrt{x}$,我们可以计算出各个$x$值对应的$y$值,并填写表格:
当$x = 0$时,$y = \sqrt{0} = 0$;
当$x = 1$时,$y = \sqrt{1} = 1$;
当$x = 4$时,$y = \sqrt{4} = 2$;
当$x = 9$时,$y = \sqrt{9} = 3$;
当$x = 16$时,$y = \sqrt{16} = 4$。
(3) 根据表格中的数值,我们可以在坐标系中描出这些点,并尝试画出这个函数的图象。
由于这是一个算术平方根函数,其图象是一个开口向上的抛物线的一部分(即其右半部分),且顶点在原点。
【答案】:
(1) $y = \sqrt{x}$;$x \geq 0$。
(2)
| $x$ | 0 | 1 | 4 | 9 | 16 |
| --- | --- | --- | --- | --- | --- |
| $y$ | 0 | 1 | 2 | 3 | 4 |
(3) 图象略(根据表格中的数值在坐标系中描点并连线,得到开口向上的抛物线的一部分,即其右半部分)。
(1) 根据题意,$y$是$x$的算术平方根,所以函数表达式为$y = \sqrt{x}$。
由于算术平方根的定义域为非负数,所以自变量$x$的取值范围是$x \geq 0$。
(2) 根据函数表达式$y = \sqrt{x}$,我们可以计算出各个$x$值对应的$y$值,并填写表格:
当$x = 0$时,$y = \sqrt{0} = 0$;
当$x = 1$时,$y = \sqrt{1} = 1$;
当$x = 4$时,$y = \sqrt{4} = 2$;
当$x = 9$时,$y = \sqrt{9} = 3$;
当$x = 16$时,$y = \sqrt{16} = 4$。
(3) 根据表格中的数值,我们可以在坐标系中描出这些点,并尝试画出这个函数的图象。
由于这是一个算术平方根函数,其图象是一个开口向上的抛物线的一部分(即其右半部分),且顶点在原点。
【答案】:
(1) $y = \sqrt{x}$;$x \geq 0$。
(2)
| $x$ | 0 | 1 | 4 | 9 | 16 |
| --- | --- | --- | --- | --- | --- |
| $y$ | 0 | 1 | 2 | 3 | 4 |
(3) 图象略(根据表格中的数值在坐标系中描点并连线,得到开口向上的抛物线的一部分,即其右半部分)。
查看更多完整答案,请扫码查看


