《2025年阳光学业评价九年级数学上册人教版》

3. 点O为$\triangle ABC$的外心,已知$\angle ACB= 50°,则\angle AOB= $100°.

答案： 解：
∵点O为△ABC的外心
∴O是△ABC外接圆的圆心
∵∠ACB=50°
∴∠AOB=2∠ACB=2×50°=100°
100

4. 在用反证法证明命题：“已知$\triangle ABC,$AB= AC,求证：$\angle B$＜90°”时,第一步应先假设(B).
$A.\angle B＞90°$
$B.\angle B≥90°$
$C.\angle B= 90°$
D.AB≠AC

答案： 【解析】：
本题考查反证法的使用。
反证法是一种通过假设某个命题的反面成立，然后推导出矛盾或不可能的情况，从而证明原命题成立的方法。
在本题中，原命题是“已知$\triangle ABC,AB= AC$，求证：$\angle B＜90°$”。
根据反证法的使用，我们首先需要假设原命题的反面成立，即假设$\angle B$不小于$90°$。
由于题目中的选项是给出了一些可能的假设，我们需要选择一个最符合“$\angle B$不小于$90°$”的选项。
观察选项，我们可以看到：
A.$\angle B＞90°$，这只是$\angle B$大于$90°$的情况，没有包括$\angle B=90°$的情况，所以不符合。
B. $\angle B≥90°$，这表示$\angle B$大于或等于$90°$，完全符合我们的假设。
C. $\angle B= 90°$，这只是$\angle B$等于$90°$的情况，没有包括$\angle B$大于$90°$的情况，所以不符合。
D. $AB≠AC$，这与原命题的条件$AB=AC$相矛盾，且与原命题的结论无关，所以不符合。
因此，我们应选择B选项，即假设$\angle B≥90°$。
【答案】：
B

5. 在平面直角坐标系中,$\triangle ABC$的位置如图所示.

(1)作出$\triangle ABC的外接圆\odot D；$
(2)直接写出点D的坐标为 ；
$(3)\triangle ABC$外接圆的半径长为直接写出结果).

答案：

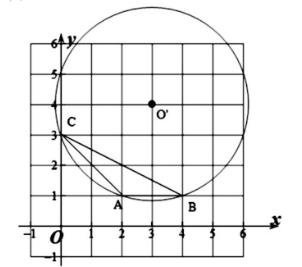
(3,4)  $\sqrt {10}$

6. 已知菱形ABCD的对角线AC,BD交于点E,以AB为直径作$\odot O,$则点E与$\odot O$的位置关系为点E在$\odot O$上.

答案： 解：连接OE。
∵四边形ABCD是菱形，
∴E为AC中点。
∵AB为$\odot O$直径，
∴O为AB中点。
∴OE是△ABC的中位线，
∴OE=$\frac{1}{2}$BC。
∵菱形ABCD中AB=BC，
∴OE=$\frac{1}{2}$AB。
∵$\odot O$半径为$\frac{1}{2}$AB，
∴点E在$\odot O$上。
答案：点E在$\odot O$上。

7. 如图,在$\triangle ABC$中,BC= 12 cm,AB= AC,$\angle BAC= 120°.(1)作\triangle ABC$的外接圆(保留作图痕迹,不写作法)；
(2)求它的外接圆直径.

答案：
(1) 图略（分别作AB、AC的垂直平分线，交于点O，以O为圆心，OA为半径作圆）。
(2) 解：连接OA、OB，OA交BC于点D。
∵AB=AC，O为外接圆圆心，
∴OA垂直平分BC，∠BAO=∠CAO=60°，BD=BC/2=6cm。
∵OA=OB，
∴△OAB为等边三角形，∠OBA=60°。
在Rt△ABD中，∠ABD=30°，
cos∠ABD=BD/AB，AB=BD/cos30°=6/(√3/2)=4√3 cm。
∴OA=AB=4√3 cm，外接圆直径为8√3 cm。
答：外接圆直径为8√3 cm。

8. 如图,D为等边三角形ABC的边BC的中点,AB= 2,动点M满足$AM\perp CM.(1)$求证：点A,D,C,M在同一个圆上；
(2)连接BM,求线段BM的最大值与最小值.

答案：
(1)证明：取AC的中点O，连接OD，OM。
∵△ABC是等边三角形，D为BC中点，
∴AD⊥BC，即∠ADC=90°。
∵AM⊥CM，
∴∠AMC=90°。
∴OA=OC=OD=OM（直角三角形斜边中线等于斜边一半）。
∴点A，D，C，M在以O为圆心，AC为直径的圆上。
(2)解：由
(1)知，点M在以AC为直径的圆上，AC=AB=2，
∴圆O半径为1，OA=OC=1。
连接BO，在等边△ABC中，AD⊥BC，AB=2，BD=1，
∴AD=√(AB²-BD²)=√3，OD=1/2AD=√3/2（D为BC中点，O为AC中点，OD为△ABC中位线）。
BO=√(BD²+OD²)=√(1²+(√3/2)²)=√(1+3/4)=√7/2。
当M在BO延长线与圆O交点时，BM最大，BM=BO+OM=√7/2+1=(√7+2)/2；
当M在OB与圆O交点时，BM最小，BM=BO-OM=√7/2-1=(√7-2)/2。
∴BM的最大值为(√7+2)/2，最小值为(√7-2)/2。

1. 已知圆的半径为6.5 cm,如果一条直线与圆心的距离为4.5 cm,那么这条直线与圆有2个交点.

答案： 解：已知圆的半径 $ r = 6.5 \, cm $，直线与圆心的距离 $ d = 4.5 \, cm $。
因为 $ d = 4.5 \, cm ＜ r = 6.5 \, cm $，
所以直线与圆相交，有 2 个交点。
答案：2