第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 下列说法中正确的是(
A.全等的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称
C
).A.全等的两个图形成中心对称
B.成中心对称的两个图形必重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称
答案:
【解析】:
本题考察的是对中心对称图形的理解。
A选项:全等的两个图形并不意味着它们一定中心对称,因为全等只要求两个图形能够完全重合,但并未规定重合的方式,所以A选项错误。
B选项:成中心对称的两个图形在未经旋转或平移等操作前,并不一定会重合,它们只是关于某点中心对称,所以B选项错误。
C选项:根据中心对称的定义,两个中心对称的图形一定是全等的,所以C选项正确。
D选项:旋转后能够重合的两个图形并不一定就是中心对称,因为旋转的角度和中心点并未明确,所以D选项错误。
【答案】:
C
本题考察的是对中心对称图形的理解。
A选项:全等的两个图形并不意味着它们一定中心对称,因为全等只要求两个图形能够完全重合,但并未规定重合的方式,所以A选项错误。
B选项:成中心对称的两个图形在未经旋转或平移等操作前,并不一定会重合,它们只是关于某点中心对称,所以B选项错误。
C选项:根据中心对称的定义,两个中心对称的图形一定是全等的,所以C选项正确。
D选项:旋转后能够重合的两个图形并不一定就是中心对称,因为旋转的角度和中心点并未明确,所以D选项错误。
【答案】:
C
2. 如图,△ABC和△A'B'C'关于点O成中心对称,则下列结论不一定成立的是(
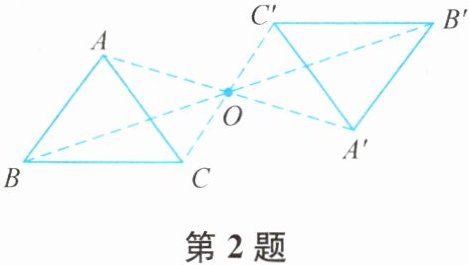
A.点A与点A'是对称点
B.BO= B'O
C.AB//A'B'
D.∠ACB= ∠C'A'B'
D
).
A.点A与点A'是对称点
B.BO= B'O
C.AB//A'B'
D.∠ACB= ∠C'A'B'
答案:
【解析】:本题可根据中心对称的性质,逐一分析选项。
中心对称的性质:成中心对称的两个图形,对应点所连线段都经过对称中心,而且被对称中心平分;成中心对称的两个图形是全等图形,对应线段相等,对应角相等,对应线段平行(或在同一直线上)。
选项A:点A与点A'是对称点
根据中心对称的定义,把一个图形绕着某一个点旋转$180^{\circ}$,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。
因为$\triangle ABC$和$\triangle A'B'C'$关于点$O$成中心对称,所以点$A$与点$A'$是对称点,该选项成立。
选项B:$BO = B'O$
由中心对称的性质可知,成中心对称的两个图形,对应点所连线段都经过对称中心,而且被对称中心平分。
因为点$B$与点$B'$是对应点,点$O$是对称中心,所以$BO = B'O$,该选项成立。
选项C:$AB// A'B'$
根据中心对称的性质,成中心对称的两个图形对应线段平行(或在同一直线上)。
因为$AB$与$A'B'$是对应线段,所以$AB// A'B'$,该选项成立。
选项D:$\angle ACB = \angle C'A'B'$
由于$\triangle ABC$和$\triangle A'B'C'$关于点$O$成中心对称,那么这两个三角形全等,全等三角形的对应角相等,所以$\angle ACB$的对应角应该是$\angle A'C'B'$,即$\angle ACB = \angle A'C'B'$,而不是$\angle C'A'B'$,该选项不一定成立。
综上,答案选D。
【答案】:D
中心对称的性质:成中心对称的两个图形,对应点所连线段都经过对称中心,而且被对称中心平分;成中心对称的两个图形是全等图形,对应线段相等,对应角相等,对应线段平行(或在同一直线上)。
选项A:点A与点A'是对称点
根据中心对称的定义,把一个图形绕着某一个点旋转$180^{\circ}$,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。
因为$\triangle ABC$和$\triangle A'B'C'$关于点$O$成中心对称,所以点$A$与点$A'$是对称点,该选项成立。
选项B:$BO = B'O$
由中心对称的性质可知,成中心对称的两个图形,对应点所连线段都经过对称中心,而且被对称中心平分。
因为点$B$与点$B'$是对应点,点$O$是对称中心,所以$BO = B'O$,该选项成立。
选项C:$AB// A'B'$
根据中心对称的性质,成中心对称的两个图形对应线段平行(或在同一直线上)。
因为$AB$与$A'B'$是对应线段,所以$AB// A'B'$,该选项成立。
选项D:$\angle ACB = \angle C'A'B'$
由于$\triangle ABC$和$\triangle A'B'C'$关于点$O$成中心对称,那么这两个三角形全等,全等三角形的对应角相等,所以$\angle ACB$的对应角应该是$\angle A'C'B'$,即$\angle ACB = \angle A'C'B'$,而不是$\angle C'A'B'$,该选项不一定成立。
综上,答案选D。
【答案】:D
3. 为培养学生利用现代信息技术解决数学问题的能力,区数学教研室在本学期组织辖区内初中生开展了“运用网络画板,探寻美丽的数学世界”比赛活动. 下列图形是部分参赛作品,其中是中心对称图形的是(
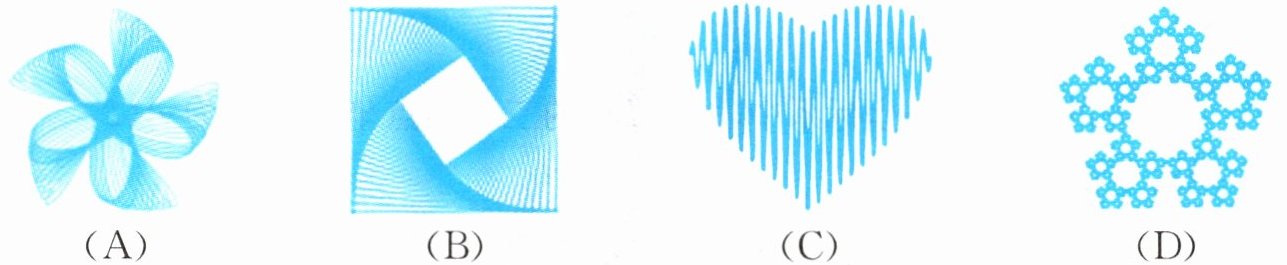
A.
B.
C.
D.
B
).
A.
B.
C.
D.
答案:
【解析】:本题考查中心对称图形的定义:在平面内,把一个图形绕着某个点旋转$180{}^{\circ }$,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
根据定义对选项逐一分析:
选项A:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
选项B:绕着正方形中心旋转$180{}^{\circ }$后,能与原图形重合,是中心对称图形。
选项C:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
选项D:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
【答案】:B
根据定义对选项逐一分析:
选项A:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
选项B:绕着正方形中心旋转$180{}^{\circ }$后,能与原图形重合,是中心对称图形。
选项C:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
选项D:绕着某点旋转$180{}^{\circ }$后,不能与原图形重合,不是中心对称图形。
【答案】:B
4. 如图,△ABC和△DEF关于点O成中心对称,则△ABC绕点O旋转
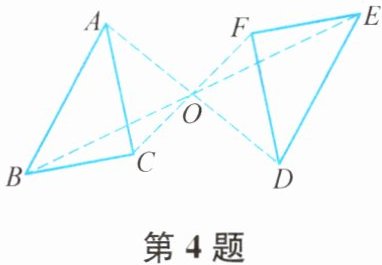
180
°可到达△DEF,且AO:OD=1:1
.
答案:
【解析】:
本题考查中心对称的性质,中心对称的定义是,在平面内,把一个图形绕着某个点旋转$180^{\circ}$ ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
根据中心对称的性质可知,$\triangle ABC$绕点$O$旋转$180^{\circ}$可到达$\triangle DEF$。
同时,因为点$A$和点$D$是关于点$O$成中心对称的,所以$AO = OD$,那么$AO:OD = 1:1$。
【答案】: 180;1:1
本题考查中心对称的性质,中心对称的定义是,在平面内,把一个图形绕着某个点旋转$180^{\circ}$ ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
根据中心对称的性质可知,$\triangle ABC$绕点$O$旋转$180^{\circ}$可到达$\triangle DEF$。
同时,因为点$A$和点$D$是关于点$O$成中心对称的,所以$AO = OD$,那么$AO:OD = 1:1$。
【答案】: 180;1:1
查看更多完整答案,请扫码查看


