《2025年阳光学业评价九年级数学上册人教版》

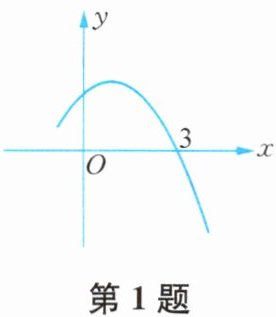
1. 已知函数$y= -x^2+2x+k$的部分图象如图所示,则$k= $3.

答案： 【解析】：
由图可知，二次函数$y= -x^2+2x+k$的图象过点$(3,0)$，
将点$(3,0)$代入二次函数$y= -x^2+2x+k$中，可得：
$0=-3^{2}+2× 3+k$。
化简得：
$0 = -9 + 6 + k$，
$0 = -3 + k$，
解得$k = 3$。
【答案】：
$3$。

2. 某一型号飞机着陆后滑行的距离$y$(单位：m)与滑行时间$x$(单位：s)之间的函数解析式是$y= 60x-1.5x^2$,该型号飞机着陆后滑行600m才能停下来.

答案： 解：$y=60x-1.5x^2=-1.5x^2+60x$，
$a=-1.5$，$b=60$，$c=0$，
$\because a=-1.5＜0$，
$\therefore$抛物线开口向下，函数有最大值，
当$x=-\dfrac{b}{2a}=-\dfrac{60}{2×(-1.5)}=20$时，
$y_{max}=\dfrac{4ac-b^2}{4a}=\dfrac{0-60^2}{4×(-1.5)}=600$，
即该型号飞机着陆后滑行$600$m才能停下来.
600

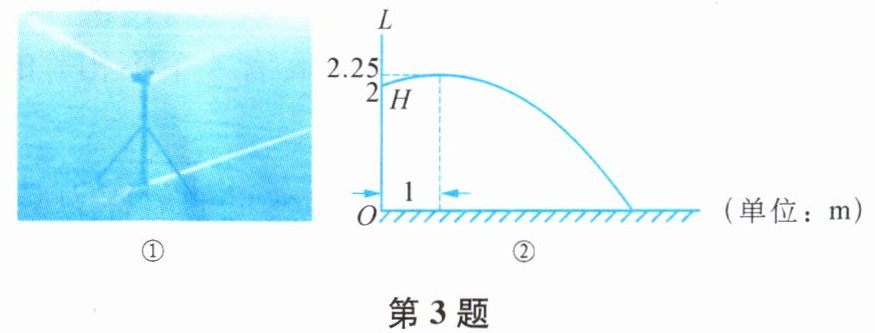
3. 如图①为喷灌系统,工作时,其侧面示意图如图②所示. 升降杆$OL$垂直于地面,喷射的水柱呈抛物线型,喷头$H$能在升降杆上调整高度,将喷头调整至离地面2 m高时,喷射的水柱在距升降杆1 m处达到最高,高度为2.25 m,此时喷射的水柱落地点与$O$的距离为4m.

答案： 【解析】：本题考查了二次函数在实际问题中的应用，需要根据已知条件建立二次函数模型，再通过求解二次函数得到水柱落地点的距离。
已知喷头$H$离地面$2m$高，即$H$点坐标为$(0,2)$，喷射的水柱在距升降杆$1m$处达到最高，高度为$2.25m$，所以抛物线的顶点坐标为$(1,2.25)$。
设抛物线的解析式为$y = a(x - 1)^2 + 2.25$（顶点式），把$H(0,2)$代入可得：
$2=a(0 - 1)^2 + 2.25$
$2=a + 2.25$
解得$a = -0.25$。
所以抛物线的解析式为$y = -0.25(x - 1)^2 + 2.25$。
当水柱落地时，$y = 0$，即$0 = -0.25(x - 1)^2 + 2.25$，
$-0.25(x - 1)^2=-2.25$
$(x - 1)^2 = 9$
$x - 1 = \pm3$
解得$x_1 = 4$，$x_2 = -2$（距离不能为负，舍去）。
因为$O$点为坐标原点，所以喷射的水柱落地点与$O$的距离为$4m$。
【答案】：$4$

4. 如图,在$\triangle ABC$中,$\angle B= 90^{\circ}$,$AB= 6\ cm$,$BC= 12\ cm$. 动点$P从A点开始沿AB向B$点以1 cm/s的速度运动(不与$B$点重合),动点$Q从B点开始沿BC$以2 cm/s的速度向$C$点运动(不与$C$重合). 如果$P$,$Q$同时出发,那么四边形$APQC$的面积最小时,要经过3s.

答案： 【解析】：
本题考查了二次函数的最值问题，根据题意表示出四边形$APQC$的面积是解题的关键。
设运动时间为$t$秒，则$AP=t$，$PB=6-t$，$BQ=2t$，$QC=12-2t$，
利用三角形面积公式表示出$\triangle ABC$和$\triangle PBQ$的面积，
进而表示出四边形$APQC$的面积，
最后根据二次函数的性质确定面积最小时的时间。
【答案】：
解：设运动时间为$t$秒，四边形$APQC$的面积为$S$，
$\because AP=t$，$PB=6-t$，$BQ=2t$，$QC=12-2t$，
$\therefore S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}×6×12=36$，
$S_{\triangle PBQ}=\frac{1}{2}PB\cdot BQ=\frac{1}{2}(6-t)\cdot2t=-t^2+6t$，
$\therefore S=S_{\triangle ABC}-S_{\triangle PBQ}=36-(-t^2+6t)=t^2-6t+36$，
$\because S=t^2-6t+36=(t-3)^2+27$，
$\therefore$当$t=3$时，$S$取得最小值，最小值为$27$，
即运动时间为$3$秒时，四边形$APQC$的面积最小。
故答案为$3$。

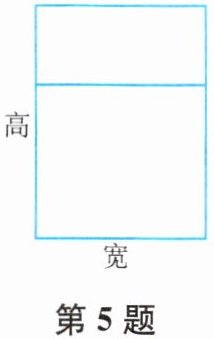
5. 有一长为7.5 m的木料,做成如图所示的“日”字形窗框,设窗的宽为$x\ m$,窗的面积为$y\ m^2$,则$y关于x$的函数解析式为$y = -\frac{3}{2}x^2 + \frac{15}{4}x$,其自变量$x$的取值范围是$0\lt x\lt2.5$.

答案： 【解析】：
本题主要考查根据实际问题列二次函数关系式及求自变量的取值范围。
窗框由长为$7.5m$的木料做成，是“日”字形，设窗的宽为$xm$，需要先表示出窗的高，再根据长方形面积公式列出函数解析式，最后根据实际情况确定自变量的取值范围。
求窗的高：
“日”字形窗框有三条横档，两条竖档，已知窗的宽为$xm$，设窗的高为$hm$。
因为木料长$7.5m$，所以可得$3x + 2h = 7.5$，
移项可得$2h = 7.5 - 3x$，
两边同时除以$2$，解得$h=\frac{7.5 - 3x}{2}$。
列函数解析式：
根据长方形的面积公式$S = 长×宽$，已知窗的宽为$xm$，高为$\frac{7.5 - 3x}{2}m$，所以窗的面积$y = x×\frac{7.5 - 3x}{2}$，
化简可得：
$y=\frac{7.5x - 3x^2}{2}=-\frac{3}{2}x^2 + \frac{15}{4}x$。
求自变量$x$的取值范围：
因为窗的宽$x\gt0$，同时窗的高$h=\frac{7.5 - 3x}{2}\gt0$。
解不等式$\frac{7.5 - 3x}{2}\gt0$，两边同时乘以$2$得$7.5 - 3x\gt0$，
移项可得$3x\lt7.5$，
两边同时除以$3$，解得$x\lt2.5$。
所以自变量$x$的取值范围是$0\lt x\lt2.5$。
【答案】：$y = -\frac{3}{2}x^2 + \frac{15}{4}x$；$0\lt x\lt2.5$。

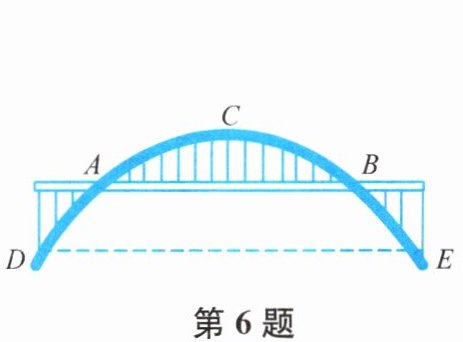
6. 某地一座抛物线形拱桥如图所示,拱桥在竖直平面内与水平桥面相交于$A$,$B$两点,拱桥最高点$C到AB$的距离为9 m,$AB= 36\ m$,$D$,$E$为拱桥底部的两点,且$DE// AB$,点$E到直线AB$的距离为7 m,则$DE$的长为48m.

答案： 解：以AB所在直线为x轴，AB中点为原点建立直角坐标系。
则A(-18,0)，B(18,0)，C(0,9)。
设抛物线解析式为$y=ax^2 + 9$，
将B(18,0)代入得：$0 = a×18^2 + 9$，解得$a=-\frac{1}{36}$，
∴抛物线解析式为$y=-\frac{1}{36}x^2 + 9$。
点E到AB距离为7m，即E点纵坐标为-7，
令$y=-7$，则$-7=-\frac{1}{36}x^2 + 9$，
$\frac{1}{36}x^2=16$，$x^2=576$，$x=±24$，
∴D(-24,-7)，E(24,-7)，
DE=24 - (-24)=48(m)。
答案：48