第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
6. 已知二次函数 $ y= ax^2 $,下列说法不正确的是(
A.对称轴为 $ y $ 轴
B.当 $ a<0 $,$ x≠0 $ 时,$ y $ 总为负值
C.当 $ a>0 $ 时,$ y $ 有最小值 0
D.当 $ a<0 $,$ x<0 $ 时,$ y $ 随 $ x $ 的增大而减小
D
).A.对称轴为 $ y $ 轴
B.当 $ a<0 $,$ x≠0 $ 时,$ y $ 总为负值
C.当 $ a>0 $ 时,$ y $ 有最小值 0
D.当 $ a<0 $,$ x<0 $ 时,$ y $ 随 $ x $ 的增大而减小
答案:
【解析】:
本题主要考察二次函数$y = ax^2$的图象和性质。
A. 对于二次函数$y = ax^2$,其对称轴为$y$轴,这是该函数的基本性质,所以A选项正确。
B. 当$a<0$时,函数图象开口向下,顶点在原点。因此,当$x≠0$时,$y$的值总是小于0,即$y$总为负值。所以B选项正确。
C. 当$a>0$时,函数图象开口向上,顶点在原点。因此,函数的最小值为0,当$x=0$时取得。所以C选项正确。
D. 当$a<0$时,函数图象开口向下。对于$x<0$的部分,随着$x$的增大(即$x$从更小的负数逐渐增大到0),$y$的值实际上是增大的(因为函数图象在$x<0$时是上升的)。所以D选项的描述是错误的。
综上所述,不正确的说法是D。
【答案】:
D
本题主要考察二次函数$y = ax^2$的图象和性质。
A. 对于二次函数$y = ax^2$,其对称轴为$y$轴,这是该函数的基本性质,所以A选项正确。
B. 当$a<0$时,函数图象开口向下,顶点在原点。因此,当$x≠0$时,$y$的值总是小于0,即$y$总为负值。所以B选项正确。
C. 当$a>0$时,函数图象开口向上,顶点在原点。因此,函数的最小值为0,当$x=0$时取得。所以C选项正确。
D. 当$a<0$时,函数图象开口向下。对于$x<0$的部分,随着$x$的增大(即$x$从更小的负数逐渐增大到0),$y$的值实际上是增大的(因为函数图象在$x<0$时是上升的)。所以D选项的描述是错误的。
综上所述,不正确的说法是D。
【答案】:
D
7. 已知点 $ (x_1,y_1) $,$ (x_2,y_2) $,$ (x_3,y_3) $ 都在函数 $ y= -2x^2 $ 的图象上,且 $ x_1>x_2>x_3>0 $,则(
A.$ y_1<y_2<y_3 $
B.$ y_1<y_3<y_2 $
C.$ y_3<y_2<y_1 $
D.$ y_2<y_1<y_3 $
A
).A.$ y_1<y_2<y_3 $
B.$ y_1<y_3<y_2 $
C.$ y_3<y_2<y_1 $
D.$ y_2<y_1<y_3 $
答案:
解:对于函数$y = -2x^2$,
因为$a=-2\lt0$,
所以抛物线开口向下,对称轴为$y$轴,
在对称轴右侧($x\gt0$),$y$随$x$的增大而减小。
已知$x_1>x_2>x_3>0$,
所以$y_1<y_2<y_3$。
答案:A
因为$a=-2\lt0$,
所以抛物线开口向下,对称轴为$y$轴,
在对称轴右侧($x\gt0$),$y$随$x$的增大而减小。
已知$x_1>x_2>x_3>0$,
所以$y_1<y_2<y_3$。
答案:A
8. 苹果熟了,从树上落下所经过的路程 $ s $ 与下落的时间 $ t $ 满足 $ s= \frac{1}{2}gt^2 $($ g $ 是不为 0 的常数),则 $ s $ 与 $ t $ 的函数图象大致是(
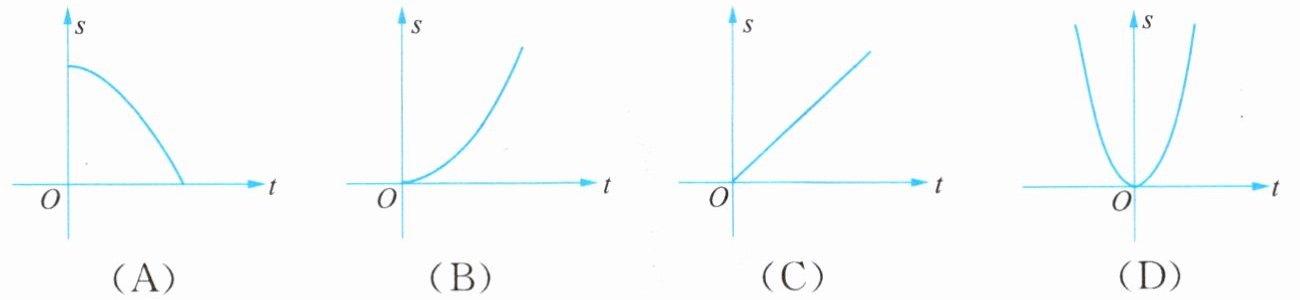
A.
B.
C.
D.
B
).
A.
B.
C.
D.
答案:
解:由题意知,$s = \frac{1}{2}gt^2$,其中$g$为不为0的常数,且时间$t \geq 0$,路程$s \geq 0$。
因为$\frac{1}{2}g$($g$为常数且不为0,实际物理情境中$g>0$)是正数,所以该函数为二次函数,且二次项系数大于0,其图象是开口向上的抛物线。
又因为$t \geq 0$,所以函数图象仅在第一象限(含原点)。
观察选项,A为开口向下的曲线且有下降部分,不符合;C为直线,是一次函数图象,不符合;D为完整抛物线(含第二象限),不符合;B为开口向上的抛物线在第一象限的部分,符合条件。
答案:B
因为$\frac{1}{2}g$($g$为常数且不为0,实际物理情境中$g>0$)是正数,所以该函数为二次函数,且二次项系数大于0,其图象是开口向上的抛物线。
又因为$t \geq 0$,所以函数图象仅在第一象限(含原点)。
观察选项,A为开口向下的曲线且有下降部分,不符合;C为直线,是一次函数图象,不符合;D为完整抛物线(含第二象限),不符合;B为开口向上的抛物线在第一象限的部分,符合条件。
答案:B
9. 若 $ y= (1-m)x^{m^2-2} $ 是二次函数,且图象开口向下.
(1)求 $ m $ 的值,并写出函数解析式;
(2)选择适当的数据填入下表,并在直角坐标系内描点,画出该二次函数的图象;

(3)结合图象,写出这个二次函数的性质.
| x | ... | | | | | ... |
| y | ... | | | | | ... |
(1)求 $ m $ 的值,并写出函数解析式;

(2)选择适当的数据填入下表,并在直角坐标系内描点,画出该二次函数的图象;

(3)结合图象,写出这个二次函数的性质.
| x | ... | | | | | ... |
| y | ... | | | | | ... |
答案:
【解析】:
(1) 首先,根据二次函数的定义,函数 $y = (1 - m)x^{m^2 - 2}$ 应该是 $x$ 的二次项,即 $m^2 - 2 = 2$。
同时,由于图像开口向下,二次项的系数 $1 - m$ 必须小于0。
解方程组:
$\begin{cases}m^2 - 2 = 2, \\1 - m < 0.\end{cases}$
解得 $m = 2$(因为 $m = -2$ 不满足 $1 - m < 0$)。
因此,函数解析式为 $y = -x^2$。
(2) 根据函数 $y = -x^2$,可以选择几个 $x$ 值,计算对应的 $y$ 值,并填入表格。
例如,可以选择 $x = -2, -1, 0, 1, 2$,计算得到 $y = -4, -1, 0, -1, -4$。
然后在直角坐标系中描出这些点,并用平滑的曲线连接,得到二次函数的图像。
填表:
| $x$ | ... | $-2$ | $-1$ | $0$ | $1$ | $2$ | ... |
| $y$ | ... | $-4$ | $-1$ | $0$ | $-1$ | $-4$ | ... |
图像为开口向下的抛物线,顶点在原点。
(3) 根据图像,可以得出以下性质:
二次函数 $y = -x^2$ 的图像是一个开口向下的抛物线。
抛物线的对称轴是 $y$ 轴(即 $x = 0$)。
抛物线的顶点坐标是 $(0, 0)$。
当 $x < 0$ 时,$y$ 随 $x$ 的增大而增大;当 $x > 0$ 时,$y$ 随 $x$ 的增大而减小。
【答案】:
(1) $m = 2$,函数解析式为 $y = -x^2$。
(2) 填表:
| $x$ | ... | $-2$ | $-1$ | $0$ | $1$ | $2$ | ... |
| $y$ | ... | $-4$ | $-1$ | $0$ | $-1$ | $-4$ | ... |
图像略。
(3) 二次函数 $y = -x^2$ 的性质:
图像是开口向下的抛物线。
对称轴是 $y$ 轴。
顶点坐标是 $(0, 0)$。
当 $x < 0$ 时,$y$ 随 $x$ 的增大而增大;当 $x > 0$ 时,$y$ 随 $x$ 的增大而减小。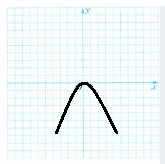
【解析】:
(1) 首先,根据二次函数的定义,函数 $y = (1 - m)x^{m^2 - 2}$ 应该是 $x$ 的二次项,即 $m^2 - 2 = 2$。
同时,由于图像开口向下,二次项的系数 $1 - m$ 必须小于0。
解方程组:
$\begin{cases}m^2 - 2 = 2, \\1 - m < 0.\end{cases}$
解得 $m = 2$(因为 $m = -2$ 不满足 $1 - m < 0$)。
因此,函数解析式为 $y = -x^2$。
(2) 根据函数 $y = -x^2$,可以选择几个 $x$ 值,计算对应的 $y$ 值,并填入表格。
例如,可以选择 $x = -2, -1, 0, 1, 2$,计算得到 $y = -4, -1, 0, -1, -4$。
然后在直角坐标系中描出这些点,并用平滑的曲线连接,得到二次函数的图像。
填表:
| $x$ | ... | $-2$ | $-1$ | $0$ | $1$ | $2$ | ... |
| $y$ | ... | $-4$ | $-1$ | $0$ | $-1$ | $-4$ | ... |
图像为开口向下的抛物线,顶点在原点。
(3) 根据图像,可以得出以下性质:
二次函数 $y = -x^2$ 的图像是一个开口向下的抛物线。
抛物线的对称轴是 $y$ 轴(即 $x = 0$)。
抛物线的顶点坐标是 $(0, 0)$。
当 $x < 0$ 时,$y$ 随 $x$ 的增大而增大;当 $x > 0$ 时,$y$ 随 $x$ 的增大而减小。
【答案】:
(1) $m = 2$,函数解析式为 $y = -x^2$。
(2) 填表:
| $x$ | ... | $-2$ | $-1$ | $0$ | $1$ | $2$ | ... |
| $y$ | ... | $-4$ | $-1$ | $0$ | $-1$ | $-4$ | ... |
图像略。
(3) 二次函数 $y = -x^2$ 的性质:
图像是开口向下的抛物线。
对称轴是 $y$ 轴。
顶点坐标是 $(0, 0)$。
当 $x < 0$ 时,$y$ 随 $x$ 的增大而增大;当 $x > 0$ 时,$y$ 随 $x$ 的增大而减小。

查看更多完整答案,请扫码查看


