第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. 每年的“双十一”购物活动,许多商家都会利用这个契机进行打折促销. 甲网店购进一件A商品的成本为50元,网上标价为80元.
(1)“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买家,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?
(2)“双十一”购物活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出1000件A商品. 在“双十一”购物活动前一天,乙网店将网上标价提高$a\%$,活动当天打五折进行促销,吸引了大量顾客,乙网店在“双十一”购物活动当天卖出的A商品数量比原来一周卖出的A商品数量增加了$2a\%$,利润达到了2万元,求乙网店在“双十一”购物活动这天打折前的网上标价.
(1)“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买家,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?
(2)“双十一”购物活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出1000件A商品. 在“双十一”购物活动前一天,乙网店将网上标价提高$a\%$,活动当天打五折进行促销,吸引了大量顾客,乙网店在“双十一”购物活动当天卖出的A商品数量比原来一周卖出的A商品数量增加了$2a\%$,利润达到了2万元,求乙网店在“双十一”购物活动这天打折前的网上标价.
答案:
(1) 解:设平均每次降价率为$x$,根据题意得:
$80(1 - x)^2 = 51.2$
$(1 - x)^2 = 0.64$
$1 - x = \pm 0.8$
解得$x_1 = 0.2 = 20\%$,$x_2 = 1.8$(不合题意,舍去)
答:平均每次降价率为$20\%$。
(2) 解:根据题意得:
标价提高后为$80(1 + a\%)$元,售价为$80(1 + a\%) × 0.5$元,
销量为$1000(1 + 2a\%)$件,利润为$20000$元。
列方程:$[80(1 + a\%) × 0.5 - 50] × 1000(1 + 2a\%) = 20000$
化简得:$[40(1 + 0.01a) - 50] × 1000(1 + 0.02a) = 20000$
$(0.4a - 10)(1 + 0.02a) = 20$
$0.008a^2 + 0.8a - 10 - 0.2a = 20$
$0.008a^2 + 0.6a - 30 = 0$
$a^2 + 75a - 3750 = 0$
解得$a_1 = 25$,$a_2 = -150$(不合题意,舍去)
打折前标价:$80(1 + 25\%) = 100$元
答:乙网店打折前的网上标价为$100$元。
(1) 解:设平均每次降价率为$x$,根据题意得:
$80(1 - x)^2 = 51.2$
$(1 - x)^2 = 0.64$
$1 - x = \pm 0.8$
解得$x_1 = 0.2 = 20\%$,$x_2 = 1.8$(不合题意,舍去)
答:平均每次降价率为$20\%$。
(2) 解:根据题意得:
标价提高后为$80(1 + a\%)$元,售价为$80(1 + a\%) × 0.5$元,
销量为$1000(1 + 2a\%)$件,利润为$20000$元。
列方程:$[80(1 + a\%) × 0.5 - 50] × 1000(1 + 2a\%) = 20000$
化简得:$[40(1 + 0.01a) - 50] × 1000(1 + 0.02a) = 20000$
$(0.4a - 10)(1 + 0.02a) = 20$
$0.008a^2 + 0.8a - 10 - 0.2a = 20$
$0.008a^2 + 0.6a - 30 = 0$
$a^2 + 75a - 3750 = 0$
解得$a_1 = 25$,$a_2 = -150$(不合题意,舍去)
打折前标价:$80(1 + 25\%) = 100$元
答:乙网店打折前的网上标价为$100$元。
1. 某学校准备建一个面积为375$m^2$的矩形游泳池,且游泳池的宽比长短10 m. 设游泳池的长为$x$ m,则可列方程(
A.$x(x-10)= 375$
B.$x(x+10)= 375$
C.$2x(2x-10)= 375$
D.$2x(2x+10)= 375$
$x(x - 10)=375$
).A.$x(x-10)= 375$
B.$x(x+10)= 375$
C.$2x(2x-10)= 375$
D.$2x(2x+10)= 375$
答案:
解:设游泳池的长为$x$ m,因为宽比长短10 m,所以宽为$(x - 10)$ m。矩形面积=长×宽,已知面积为$375 m^2$,则可列方程$x(x - 10)=375$。
答案:A
答案:A
2. 在一幅长60 cm,宽40 cm的矩形书画作品的四周镶一条金色纸边,制成一幅矩形挂图,如图所示. 如果要使整个作品的面积是2816$cm^2$,设金色纸边的宽为$x$ cm,那么$x$满足的方程是(
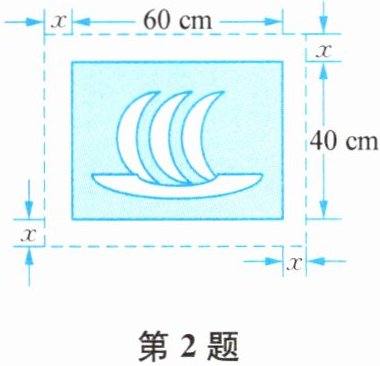
A.$(60+2x)(40+2x)= 2816$
B.$(60+x)(40+x)= 2816$
C.$(60+2x)(40+x)= 2816$
D.$(60+x)(40+2x)= 2816$
A
).[!img]
A.$(60+2x)(40+2x)= 2816$
B.$(60+x)(40+x)= 2816$
C.$(60+2x)(40+x)= 2816$
D.$(60+x)(40+2x)= 2816$
答案:
解:镶边后矩形挂图的长为$(60 + 2x)\ cm$,宽为$(40 + 2x)\ cm$,根据面积公式可得方程$(60 + 2x)(40 + 2x) = 2816$。
答案:A
答案:A
3. 某小区准备在每两幢楼房之间开辟面积为300$m^2$的一块矩形绿地,并且长比宽多10 m. 设矩形绿地的宽为$x$ m,则可列方程为
$x(x + 10) = 300$
.
答案:
解:设矩形绿地的宽为$x$ m,因为长比宽多$10$ m,所以长为$(x + 10)$ m。
矩形面积 = 长×宽,已知面积为$300 m^2$,则可列方程为:$x(x + 10) = 300$。
答案:$x(x + 10) = 300$
矩形面积 = 长×宽,已知面积为$300 m^2$,则可列方程为:$x(x + 10) = 300$。
答案:$x(x + 10) = 300$
4. 一块正方形钢板上截去3 cm宽的长方形钢条,剩下的面积是54$cm^2$,则原来这块钢板的面积是
81
$cm^2$.
答案:
【解析】:
本题主要考查一元二次方程的应用。设原正方形的边长为$x$ cm,则原正方形的面积为$x^2$ $cm^2$。
截去3cm宽的长方形钢条后,剩下的部分是一个长方形,其长为原正方形的边长$x$ cm,宽为($x-3$) cm。
根据题意,这个剩下的长方形的面积是54 $cm^2$,因此我们可以得到方程:
$x(x - 3) = 54$
展开方程得:
$x^2 - 3x - 54 = 0$
这是一个一元二次方程,我们可以使用求根公式或者因式分解法来求解。
这里我们选择因式分解法,得到:
$(x - 9)(x + 6) = 0$
解得:
$x_1 = 9, x_2 = -6$
由于边长不能为负,所以$x_2 = -6$不符合题意,舍去。
因此,原正方形的边长为9cm,所以原钢板的面积为:
$9^2 = 81 (cm^2)$
【答案】:
81
本题主要考查一元二次方程的应用。设原正方形的边长为$x$ cm,则原正方形的面积为$x^2$ $cm^2$。
截去3cm宽的长方形钢条后,剩下的部分是一个长方形,其长为原正方形的边长$x$ cm,宽为($x-3$) cm。
根据题意,这个剩下的长方形的面积是54 $cm^2$,因此我们可以得到方程:
$x(x - 3) = 54$
展开方程得:
$x^2 - 3x - 54 = 0$
这是一个一元二次方程,我们可以使用求根公式或者因式分解法来求解。
这里我们选择因式分解法,得到:
$(x - 9)(x + 6) = 0$
解得:
$x_1 = 9, x_2 = -6$
由于边长不能为负,所以$x_2 = -6$不符合题意,舍去。
因此,原正方形的边长为9cm,所以原钢板的面积为:
$9^2 = 81 (cm^2)$
【答案】:
81
查看更多完整答案,请扫码查看


