《2025年阳光学业评价九年级数学上册人教版》

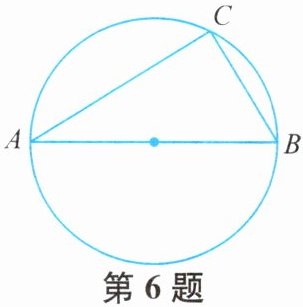
6. 如图,已知AB是△ABC外接圆的直径,∠A= 35°,则∠B的度数是55°.

答案： 解：
∵AB是△ABC外接圆的直径，
∴∠ACB=90°（直径所对的圆周角是直角）。
∵∠A=35°，
∴∠B=90°-∠A=90°-35°=55°。
55°

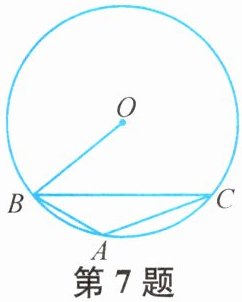
7. 如图,△ABC内接于⊙O,∠OBC= 40°,则∠A的度数为50°.

答案： 【解析】：本题可根据圆周角定理以及等腰三角形的性质来求解$\angle A$的度数。
步骤一：分析$OB$与$OC$的关系
因为$OB$、$OC$均为圆$O$的半径，根据圆的性质可知，同圆的半径相等，所以$OB = OC$。
步骤二：求出$\angle OCB$的度数
已知$\angle OBC = 40^{\circ}$，由于$OB = OC$，所以$\triangle OBC$是等腰三角形，根据等腰三角形的性质：等腰三角形的两个底角相等，可得$\angle OCB=\angle OBC = 40^{\circ}$。
步骤三：求出$\angle BOC$的度数
根据三角形内角和定理：三角形内角和为$180^{\circ}$，在$\triangle OBC$中，已知$\angle OBC = 40^{\circ}$，$\angle OCB = 40^{\circ}$，则$\angle BOC = 180^{\circ}-\angle OBC - \angle OCB=180^{\circ}-40^{\circ}-40^{\circ}=100^{\circ}$。
步骤四：求出$\angle A$的度数
根据圆周角定理：同弧所对的圆周角是圆心角的一半，因为$\angle A$是圆周角，$\angle BOC$是圆心角，且它们都对着弧$\overset{\frown}{BC}$，所以$\angle A=\frac{1}{2}\angle BOC$，将$\angle BOC = 100^{\circ}$代入可得$\angle A=\frac{1}{2}×100^{\circ}=50^{\circ}$。
【答案】：$50^{\circ}$

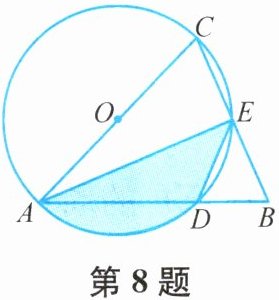
8. 如图,在△ABC中,AB= AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若AB= 3,∠BED= 45°,则阴影部分的面积为______.

$\frac{9\pi}{16}-\frac{9}{8}$

答案： 解：连接OE。
∵AC为⊙O直径，
∴∠AEC=90°。
∵AB=AC=3，
∴∠B=∠C，BE=EC。
∵∠BED=45°，∠BED=∠BAE，
∴∠BAE=45°。
∵∠AEC=90°，
∴∠EAC=∠BAE=45°，∠BAC=90°。
∴△ABC为等腰直角三角形，∠C=45°。
∵OA=OE，
∴∠OEA=∠OAE=45°，∠AOE=90°。
OA=OE=3/2。
S阴影=S扇形AOE-S△AOE= (90π×(3/2)²)/360 - (1/2)×(3/2)×(3/2)= 9π/16 - 9/8。
答案：9π/16 - 9/8

9. 如图,已知在矩形ABCD中,AB= 1,BC= $\sqrt{3}$,点P是AD边上的一个动点,连接BP,点C关于直线BP的对称点为C₁,当点P运动时,点C₁也随之运动. 若点P从点A运动到点D,则点C₁运动的路径长为$\frac{\sqrt{3}}{2}\pi$.

答案： 解：连接BC₁，由对称性质得BC₁=BC=$\sqrt{3}$，则点C₁在以B为圆心，$\sqrt{3}$为半径的圆上。
当P与A重合时，直线BP为BA，点C关于BA的对称点C₁₁与D重合，此时BC₁₁=BD。在矩形ABCD中，BD=$\sqrt{AB²+AD²}=\sqrt{1²+(\sqrt{3})²}=2$，则$\cos\angle C₁₁BA=\frac{AB}{BD}=\frac{1}{2}$，故$\angle C₁₁BA=60°$。
当P与D重合时，直线BP为BD，点C关于BD的对称点C₁₂，由对称性质知$\angle C₁₂BD=\angle CBD$。在Rt△BCD中，$\tan\angle CBD=\frac{CD}{BC}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$，故$\angle CBD=30°$，则$\angle C₁₂BA=\angle ABC - 2\angle CBD=90° - 60°=30°$。
点C₁运动的圆心角为$\angle C₁₁BC₁₂=\angle C₁₁BA + \angle C₁₂BA=60° + 30°=90°=\frac{\pi}{2}$。
路径长为$\frac{90°}{360°}×2\pi×\sqrt{3}=\frac{\sqrt{3}}{2}\pi$。
答案：$\frac{\sqrt{3}}{2}\pi$

10. 如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线$y= -\frac{3}{4}x+3$上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是______.

2√2

答案： 解：连接AQ、AP。
∵PQ是⊙A的切线，
∴AQ⊥PQ，即△APQ为直角三角形，
∴PQ² = AP² - AQ²。
∵⊙A半径AQ=1，
∴PQ² = AP² - 1，PQ = √(AP² - 1)。
当AP最小时，PQ最小。
AP最小值为点A到直线y = -3/4x + 3的距离。
直线方程化为3x + 4y - 12 = 0，A(-1,0)，
距离d = |3×(-1) + 4×0 - 12| / √(3² + 4²) = |-15| / 5 = 3。
∴AP最小值=3，
∴PQ最小值=√(3² - 1) = √8 = 2√2。
2√2

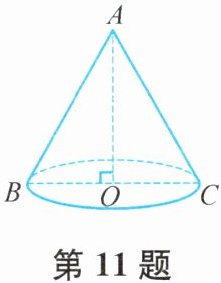
11. 某同学用纸板制作一个圆锥形漏斗,如图,圆锥的母线AC与高AO的夹角为30°,母线长为6 cm. 若不计接缝和损耗,求所需纸板的面积.(结果保留π)

答案： 解：在Rt△AOC中，∠OAC=30°，AC=6cm，
∵sin30°=OC/AC，
∴OC=AC·sin30°=6×1/2=3cm，
即圆锥底面半径r=3cm，母线长l=6cm，
所需纸板面积即为圆锥侧面积：S=πrl=π×3×6=18π(cm²)。
答：所需纸板的面积为18π cm²。