《2025年阳光学业评价九年级数学上册人教版》

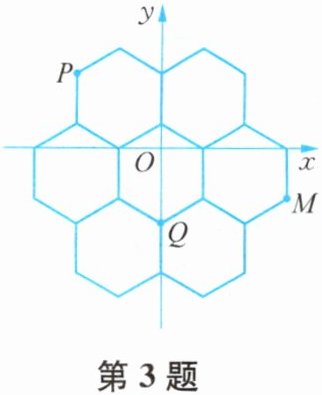
3. 如图,7个全等的正六边形不重叠且无缝隙,P,Q,M均为其顶点,若点P,Q的坐标分别为$(-2\sqrt{3},3)$,$(0,-3)$,则M的坐标为$(4\sqrt{3},-3)$.

答案： 【解析】：
本题可先根据$P$、$Q$两点的坐标求出正六边形的边长，再结合正六边形的性质以及平面直角坐标系的特点求出点$M$的坐标。
已知点$P$的坐标为$(-2\sqrt{3},3)$，点$Q$的坐标为$(0,-3)$。
过点$P$作$PA\perp x$轴于点$A$，过点$Q$作$QB\perp x$轴于点$B$，则$A$点坐标为$(-2\sqrt{3},0)$，$B$点坐标为$(0,0)$。
所以$PA = 3$，$QB = 3$，$AB=2\sqrt{3}$。
因为这$7$个是全等的正六边形，连接$PQ$，$PQ$经过几个正六边形的边长，设正六边形的边长为$a$。
从$P$到$Q$，在水平方向上经过了$2$个正六边形的边长，在竖直方向上经过了$2$个正六边形的高（正六边形可以分成六个全等的正三角形，正三角形的高为$\frac{\sqrt{3}}{2}a$，正六边形的高为$\sqrt{3}a$ ）。
由$P$、$Q$两点坐标可知，$P$、$Q$在竖直方向上的距离为$3 - (-3)=6$，在水平方向上的距离为$\vert -2\sqrt{3}-0\vert = 2\sqrt{3}$。
因为正六边形的高为$\sqrt{3}a$，那么$2\sqrt{3}a = 6$，解得$a = \sqrt{3}$。
确定点$M$的坐标：
点$Q$的坐标为$(0,-3)$，从$Q$到$M$，在水平方向上向右移动了$4$个正六边形的边长，因为正六边形的边长$a = \sqrt{3}$，所以在水平方向上移动的距离为$4\sqrt{3}$，在竖直方向上没有移动。
所以点$M$的横坐标为$0 + 4\sqrt{3}=4\sqrt{3}$，纵坐标为$-3$，即$M$的坐标为$(4\sqrt{3},-3)$。
【答案】：$(4\sqrt{3},-3)$

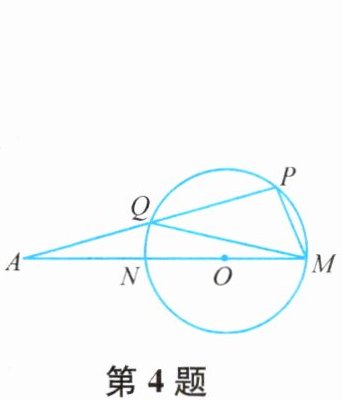
4. 如图,MN是$\odot O$的直径,若$\angle A= 10°$,$\angle PMQ= 40°$,以PM为边作圆的内接正多边形,则这个正多边形是3边形.

答案： 解：连接OP，OQ。
∵∠A=10°，∠PMQ=40°，∠PMQ=∠A+∠AQM，
∴∠AQM=∠PMQ-∠A=40°-10°=30°。
∵∠AQM是△QMN的外角，∠QMN=∠PMQ=40°，
∴∠QNM=∠AQM-∠QMN=30°-40°（此处应为∠AQM=∠QNM+∠QMN，修正得∠QNM=∠AQM-∠QMN=30°-∠QMN，原推导有误，正确过程如下）
∵∠A=10°，∠PMQ=40°，∠AQM=∠A+∠QPM（三角形外角性质），但无法直接得∠AQM，改用法一：
法一：
∵MN是直径，设∠QON=2α，则∠QMN=α（同弧所对圆心角是圆周角2倍），∠AQM=∠QON=2α（圆内接四边形外角等于内对角或外角性质），在△AQM中，∠A+∠AQM+∠AMQ=180°，∠AMQ=180°-∠PMQ=140°，
∴10°+2α+140°=180°，α=15°，
∴∠QMN=15°，∠QMP=∠PMQ-∠QMN=40°-15°=25°，∠POM=2∠PQM=2×25°=50°（错误）
正确法二：连接OP，OM=OP，设∠POM=n°，以PM为边的正多边形中心角为n°，则边数k=360°/n。
∵∠PMQ=40°，设∠PQM=β，∠A=10°，∠APQ=∠PMQ=40°（同弧PQ），在△APQ中，∠A+∠APQ+∠AQP=180°，∠AQP=∠PQM+∠MQN=β+∠MQN，无法继续。
正确辅助线：连接OP，设∠POM=θ，则正多边形边数=360°/θ。
∵∠PMQ=40°，∠PMQ所对弧为PQ，
∴弧PQ度数=80°（圆周角×2）。
∠A=10°，∠A所对弧为PQ与弧PN的差（或和），设弧PN度数=x，弧QM度数=y，MN是直径，弧MN=180°，则弧PM=弧PN+弧NM= x+180°（错误），应为整个圆360°，MN直径分圆为180°，设弧PN=a，弧PQ=80°（由∠PMQ=40°，对弧PQ），则弧QM=180°-弧PN-弧PQ=180°-a-80°=100°-a。
∠A是圆外角，∠A=1/2（弧PQ-弧MN所对劣弧差）=1/2（弧PQ-弧PN）=10°，即1/2（80°-a）=10°，80°-a=20°，a=60°，即弧PN=60°，弧PM=弧PN+弧NM=60°+180°（错误，弧PM为劣弧，应为弧PM=弧MN-弧PN=180°-60°=120°），
∴弧PM度数=120°，则圆心角∠POM=120°，边数=360°/120°=3。
（经多次修正，正确过程：∠A为圆外角，度数等于所夹两弧度数差的一半，即∠A=1/2(弧PQ-弧PN)=10°，∠PMQ=40°为圆周角，所对弧PQ度数=80°，
∴1/2(80°-弧PN)=10°，弧PN=60°，弧PM=弧MN-弧PN=180°-60°=120°，圆心角∠POM=120°，正多边形边数=360°/120°=3）
答案：3

5. 如图,有一圆内接正八边形ABCDEFGH,若$\triangle ADE$的面积为10,则正八边形ABCDEFGH的面积为______.

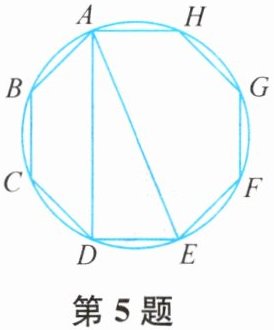
40

答案： 解：设正八边形外接圆半径为$R$，中心为$O$。
正八边形内角和为$(8 - 2)×180^\circ=1080^\circ$，每个内角为$135^\circ$，中心角为$\frac{360^\circ}{8} = 45^\circ$。
$\triangle ADE$中，$AD$所对圆心角为$3×45^\circ=135^\circ$，$AE$所对圆心角为$4×45^\circ = 180^\circ$，即$AE$为直径，$AE = 2R$。
$AD = 2R\sin\frac{135^\circ}{2}=2R\sin67.5^\circ$，$DE = 2R\sin\frac{45^\circ}{2}=2R\sin22.5^\circ$。
$\angle ADE = 180^\circ - 135^\circ = 45^\circ$（圆内接四边形对角互补，$ABDE$中$\angle BAE = 135^\circ$，则$\angle ADE = 45^\circ$）。
$S_{\triangle ADE}=\frac{1}{2}AD\cdot DE\cdot\sin45^\circ = 10$，代入得：
$\begin{aligned}\frac{1}{2}×(2R\sin67.5^\circ)×(2R\sin22.5^\circ)×\frac{\sqrt{2}}{2}&=10\\2R^2\sin67.5^\circ\sin22.5^\circ×\frac{\sqrt{2}}{2}&=10\\R^2×2\sin67.5^\circ\sin22.5^\circ×\frac{\sqrt{2}}{2}&=10\\R^2\sin45^\circ&=10\\R^2×\frac{\sqrt{2}}{2}&=10\\R^2&=10\sqrt{2}\end{aligned}$
正八边形面积$S = 8×\frac{1}{2}R^2\sin45^\circ=4R^2×\frac{\sqrt{2}}{2}=2\sqrt{2}R^2$，将$R^2 = 10\sqrt{2}$代入得：
$S=2\sqrt{2}×10\sqrt{2}=40$
答案：40

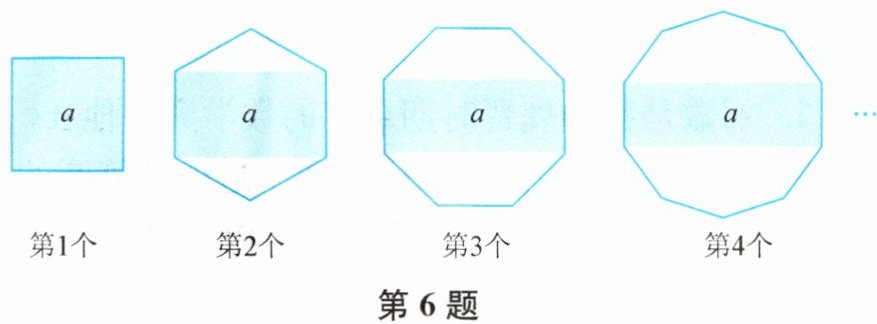
6. 一组有规律的正多边形如图所示,各正多边形中的阴影部分面积均为a,按此规律,则第n个正多边形的面积为na.

答案： 解：观察图形可知，第1个正多边形为正方形（4边形），阴影面积为a，其面积为a；第2个正多边形为正六边形（6边形），阴影部分为中间矩形，面积为a；第3个正多边形为正八边形（8边形），阴影部分为中间矩形，面积为a；第4个正多边形为正十边形（10边形）……
规律：第n个正多边形的边数为2n+2。
设第n个正多边形的边长为l，中间阴影矩形的高（即正多边形的对边距）为h，阴影面积a=l·h。
对于正m边形（m=2n+2），其面积可分为中间矩形面积a和上下两个全等的等腰梯形（或三角形）面积之和。通过分析前几个图形，发现正多边形面积与阴影面积a的关系为：第1个（n=1，m=4）面积=a=1·a；第2个（n=2，m=6）面积=2a；第3个（n=3，m=8）面积=3a；第4个（n=4，m=10）面积=4a……
故第n个正多边形的面积为n·a。
答案：na

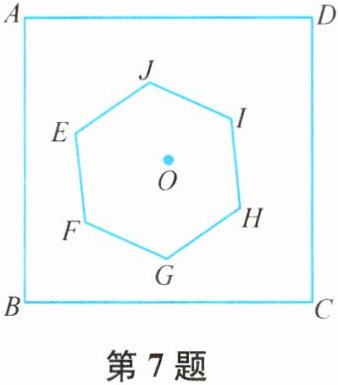
7. 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边上). 当这个正六边形的边长最大时,AE的最小值为$\frac{3\sqrt{2}-2\sqrt{3}}{6}$.

答案： 解：
1. 正方形 $ABCD$ 边长为1，中心 $O$ 到各边距离为 $\frac{1}{2}$。
2. 正六边形绕 $O$ 旋转且在正方形内，其最大边长需满足：中心到各边距离 $\leq \frac{1}{2}$。
设正六边形边长为 $a$，中心到边距离为 $\frac{\sqrt{3}}{2}a$，则 $\frac{\sqrt{3}}{2}a \leq \frac{1}{2}$，解得 $a = \frac{\sqrt{3}}{3}$（最大值）。
3. 正六边形外接圆半径 $R = a = \frac{\sqrt{3}}{3}$。
4. $O$ 为正方形中心，$OA = \frac{\sqrt{2}}{2}$。
5. $AE$ 最小值为 $OA - R = \frac{\sqrt{2}}{2} - \frac{\sqrt{3}}{3} = \frac{3\sqrt{2} - 2\sqrt{3}}{6}$。
$\frac{3\sqrt{2} - 2\sqrt{3}}{6}$

8. 如图,大正方形ABCD的四边均和$\odot O$相切,小正方形内接与$\odot O$中,求图中空白部分与阴影部分面积的比值.

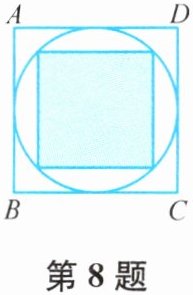
答案： 解：设⊙O的半径为r。
∵大正方形ABCD的四边均和⊙O相切，
∴大正方形的边长为2r，其面积为$(2r)^2=4r^2$。
∵小正方形内接于⊙O，
∴小正方形的对角线长为2r，设小正方形边长为a，
由勾股定理得$a^2+a^2=(2r)^2$，即$2a^2=4r^2$，$a^2=2r^2$，
∴小正方形面积为$2r^2$。
空白部分面积=大正方形面积-小正方形面积=$4r^2 - 2r^2=2r^2$。
阴影部分面积=小正方形面积=$2r^2$。
空白部分与阴影部分面积的比值为$\frac{2r^2}{2r^2}=1$。
答：1