《2025年阳光学业评价九年级数学上册人教版》

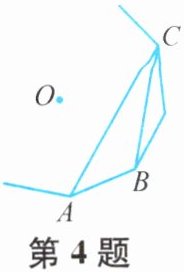
4. 正多边形的一部分如图所示,点O为正多边形的中心,若$\angle ACB= 18°$,则该正多边形的边数为(10).

A.8
B.9
C.10
D.11

答案： 解：连接OA、OB。
∵点O为正多边形的中心，
∴OA=OB，∠AOB为正多边形的中心角。
∵∠ACB=18°，且∠ACB是圆周角，∠AOB是圆心角，
∴∠AOB=2∠ACB=36°。
设正多边形边数为n，则中心角∠AOB=360°/n，
∴360°/n=36°，解得n=10。
答案：C

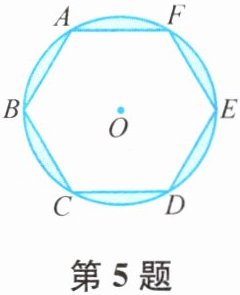
5. 如图,若$\odot O$的半径为3,六边形ABCDEF是$\odot O$的内接正六边形,求图中阴影部分的面积.

答案： 解：连接OA、OF、OC、OD。
∵六边形ABCDEF是⊙O的内接正六边形，
∴中心角∠AOF=∠COD=360°/6=60°。
∵OA=OF=OC=OD=3，
∴△AOF和△COD均为等边三角形，
∴AF=OA=3，CD=OC=3，∠OAF=∠OCD=60°。
∵正六边形ABCDEF是轴对称图形，
∴AF//CD，
∴阴影部分可拼成一个扇形，其圆心角为∠AOF+∠COD=120°。
S阴影=120°/360°×π×3²=3π。
答：图中阴影部分的面积为3π。

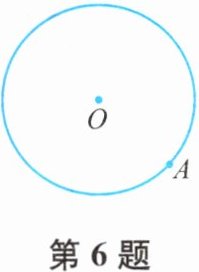
6. 如图,已知$\odot O及\odot O$上一点A.
(1)请用尺规作$\odot O$的内接正方形ABCD；(保留作图痕迹,不写作法)
(2)若$\odot O的周长等于4\pi$,求正方形ABCD的边长.

答案： 【解析】：
(1) 这一问考查的是正多边形和圆的基本作图方法，需要用尺规作出圆的内接正方形，具体步骤如下：
1. 过点A作⊙O的直径AC；
2. 再作AC的垂直平分线交⊙O于B、D两点；
3. 连接AB、BC、CD、DA，四边形ABCD即为所求的正方形。
这一问主要考查作图能力，不涉及计算。
（2）这一问考查的是圆的周长公式以及正多边形的性质，需要求出正方形ABCD的边长。
已知$\odot O$的周长为$4\pi$，根据圆的周长公式$C = 2\pi r$，可以求出半径$r$，进而求出直径$d$。
由于正方形ABCD是$\odot O$的内接正方形，正方形的对角线等于圆的直径，即$AC = d$。
根据正方形的性质，边长$a$与对角线$AC$的关系为$AC = \sqrt{2}a$，从而可以求出正方形的边长$a$。
【答案】：
(1)图略
(2)解：
因为$\odot O$的周长等于$4\pi$，
所以$2\pi r = 4\pi$，
解得$r = 2$，
则$d = 4$，即$AC = 4$。
因为正方形ABCD是$\odot O$的内接正方形，
所以$AC$是正方形ABCD的对角线，
根据正方形的性质，对角线$AC$与边长$a$的关系为$AC = \sqrt{2}a$，
所以$a = \frac{AC}{\sqrt{2}} = \frac{4}{\sqrt{2}} = 2\sqrt{2}$。
故正方形ABCD的边长为$2\sqrt{2}$。

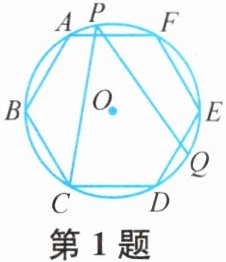
1. 如图,正六边形ABCDEF内接于$\odot O$,点P在$\widehat{AF}$上,Q是$\widehat{DE}$的中点,则$\angle CPQ$的度数为(C).

A.$30^\circ$
B.$36^\circ$
C.$45^\circ$
D.$60^\circ$

答案： 解：连接CQ，DQ。
∵正六边形ABCDEF内接于⊙O，
∴⊙O的周长被六等分，每段弧所对圆心角为60°，即$\widehat{CD}=\widehat{DE}=60^\circ$。
∵Q是$\widehat{DE}$的中点，
∴$\widehat{DQ}=\frac{1}{2}\widehat{DE}=30^\circ$，
∴$\widehat{CQ}=\widehat{CD}+\widehat{DQ}=60^\circ+30^\circ=90^\circ$。
∵点P在⊙O上，
∴∠CPQ是$\widehat{CQ}$所对的圆周角，
∴∠CPQ=$\frac{1}{2}\widehat{CQ}=\frac{1}{2}×90^\circ=45^\circ$。
答案：C

2. 同圆的内接正三角形与内接正六边形面积的比是(1:2).
A.$1:\sqrt{2}$
B.$1:2$
C.$\sqrt{2}:\sqrt{3}$
D.$1:3$

答案： 解：设圆的半径为$R$。
内接正三角形：
中心角$\alpha_3 = \frac{360^\circ}{3} = 120^\circ$，
边长$a_3 = 2R\sin\frac{120^\circ}{2} = 2R\sin60^\circ = \sqrt{3}R$，
边心距$r_3 = R\cos\frac{120^\circ}{2} = R\cos60^\circ = \frac{1}{2}R$，
面积$S_3 = \frac{1}{2} × 3 × a_3 × r_3 = \frac{1}{2} × 3 × \sqrt{3}R × \frac{1}{2}R = \frac{3\sqrt{3}}{4}R^2$。
内接正六边形：
中心角$\alpha_6 = \frac{360^\circ}{6} = 60^\circ$，
边长$a_6 = 2R\sin\frac{60^\circ}{2} = 2R\sin30^\circ = R$，
边心距$r_6 = R\cos\frac{60^\circ}{2} = R\cos30^\circ = \frac{\sqrt{3}}{2}R$，
面积$S_6 = \frac{1}{2} × 6 × a_6 × r_6 = \frac{1}{2} × 6 × R × \frac{\sqrt{3}}{2}R = \frac{3\sqrt{3}}{2}R^2$。
$S_3:S_6 = \frac{3\sqrt{3}}{4}R^2 : \frac{3\sqrt{3}}{2}R^2 = 1:2$。
答案：B