《2025年阳光学业评价九年级数学上册人教版》

1. 已知$\triangle ABC$的三边长分别为6 cm,8 cm,10 cm,则这个三角形的外接圆的面积为25π$cm^2$,内切圆的面积为4π$cm^2$.(结果用含$\pi$的代数式表示)

答案： 解：
∵ $6^2 + 8^2 = 10^2$，
∴ $\triangle ABC$ 是直角三角形，斜边长为 10 cm。
外接圆面积：
直角三角形外接圆半径 $R = \frac{10}{2} = 5$ cm，
面积 $S_{外接圆} = \pi R^2 = \pi × 5^2 = 25\pi$ $cm^2$。
内切圆面积：
设内切圆半径为 $r$，
由面积法：$\frac{1}{2} × 6 × 8 = \frac{1}{2} × (6 + 8 + 10)r$，
解得 $r = 2$ cm，
面积 $S_{内切圆} = \pi r^2 = \pi × 2^2 = 4\pi$ $cm^2$。
25π，4π

2. (1)若$O为\triangle ABC$的外心,且$\angle BOC= 60°$,则$\angle BAC= $30°或150°；
(2)若$I为\triangle ABC$的内心,且$\angle BIC= 115°$,则$\angle BAC= $50°.

答案：
(1)解：当点A在优弧BC上时，∠BAC=1/2∠BOC=30°；当点A在劣弧BC上时，∠BAC=180°-1/2∠BOC=150°。故∠BAC=30°或150°。
(2)解：
∵I为△ABC的内心，
∴∠IBC=1/2∠ABC，∠ICB=1/2∠ACB。
∵∠BIC=115°，
∴∠IBC+∠ICB=180°-115°=65°，
∴∠ABC+∠ACB=2×65°=130°，
∴∠BAC=180°-130°=50°。故∠BAC=50°。

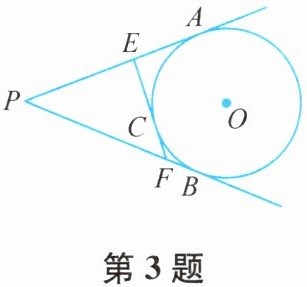
3. 如图,已知$PA$,$PB分别与\odot O相切于点A$,$B$,$\odot O的切线EF分别交PA$,$PB于点E$,$F$,切点$C在\overset{\frown}{AB}$上,若$PA$的长为2,则$\triangle PEF$的周长是4.
]

答案： 【解析】：本题可根据切线长定理来求解$\triangle PEF$的周长。
切线长定理为：从圆外一点引圆的两条切线，它们的切线长相等。
在本题中，$PA$、$PB$分别与$\odot O$相切于点$A$、$B$，则$PA = PB = 2$；$\odot O$的切线$EF$分别交$PA$、$PB$于点$E$、$F$，切点$C$在$\overset{\frown}{AB}$上，则$EA = EC$，$FB = FC$。
$\triangle PEF$的周长为$PE + EF + PF$，将$EF$转化为$EC + FC$，则$\triangle PEF$的周长可表示为$PE + EC + FC + PF$，再根据$EA = EC$，$FB = FC$，进一步转化为$PE + EA + FB + PF$，即$(PE + EA)+(PF + FB)$，也就是$PA + PB$。
已知$PA = 2$，$PB = 2$，所以$\triangle PEF$的周长为$PA + PB = 2 + 2 = 4$。
【答案】：$4$

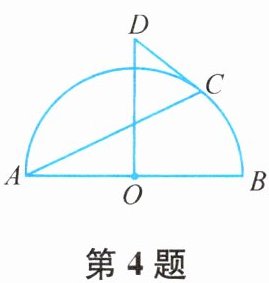
4. 如图,$AB是半圆O$的直径,点$C$在半圆上,$CD$是半圆的切线,且$OD\perp AB$,若$\angle CAB= 28°$,则$\angle D$的度数为56°.
]

答案： 解：连接OC。
∵AB是半圆O的直径，∠CAB=28°，
∴∠ACB=90°（直径所对的圆周角是直角），
∠COB=2∠CAB=56°（同弧所对的圆心角是圆周角的2倍）。
∵OD⊥AB，
∴∠AOD=∠BOD=90°，
∴∠COD=∠BOD - ∠COB=90° - 56°=34°。
∵CD是半圆的切线，
∴OC⊥CD（切线的性质），
∴∠OCD=90°，
∴∠D=90° - ∠COD=90° - 34°=56°。
56°

5. 我国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说：“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示.
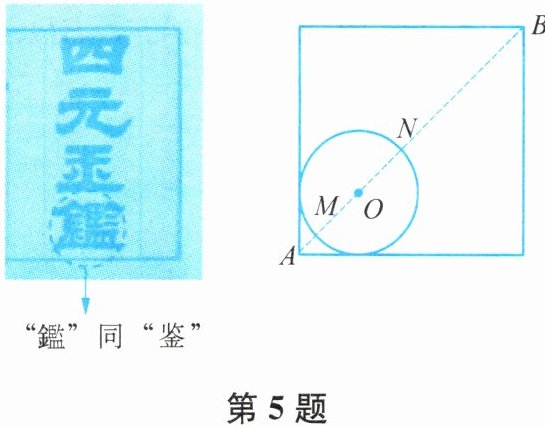
问题：此图中,正方形一条对角线$AB与\odot O相交于点M$,$N$(点$N在点M$的右上方),若$AB$的长度为10丈,$\odot O$的半径为2丈,则$BN$的长度为$8-2\sqrt{2}$丈.
]

答案： 解：设正方形左下角顶点为C，以点C为原点，正方形的边为坐标轴建立平面直角坐标系。
∵圆与正方形一角两边相切，半径为2丈，
∴圆心O的坐标为(2,2)。
∵AB是正方形对角线，长度为10丈，
∴点A(0,0)，点B(10,10)，直线AB的解析式为y=x。
点O到直线AB的距离d=$\frac{|2-2|}{\sqrt{1^2+(-1)^2}}=0$，即圆心O在直线AB上。
∴AO=$\sqrt{(2-0)^2+(2-0)^2}=2\sqrt{2}$，ON=OM=2。
∵点N在点M右上方，
∴BN=AB-AO-ON=10-2$\sqrt{2}$-2=8-2$\sqrt{2}$。
答案：$8-2\sqrt{2}$