《2025年阳光学业评价七年级数学上册人教版》

5. 先化简,再求值：
(1)$5x^2 + 4 - 3x^2 - 5x - 2x^2 - 5 + 6x$,其中$x = -3$；
(2)$2a - \frac{5}{3}a^2 + 1 + 3ab - \frac{1}{6}a^2 - 2ab + \frac{11}{6}a^2 - 2a - 3$,其中$a = \frac{1}{2}$,$b = 3$.

答案：
(1)
原式：$5x^2 + 4 - 3x^2 - 5x - 2x^2 - 5 + 6x$
合并同类项：
$=(5x^2 - 3x^2 - 2x^2) + (-5x + 6x) + (4 - 5)$
$= 0 + x - 1$
$= x - 1$
当 $x = -3$ 时，
原式 $= -3 - 1 = -4$
(2)
原式：$2a - \frac{5}{3}a^2 + 1 + 3ab - \frac{1}{6}a^2 - 2ab + \frac{11}{6}a^2 - 2a - 3$
合并同类项：
$= (-\frac{5}{3}a^2 - \frac{1}{6}a^2 + \frac{11}{6}a^2) + (2a - 2a) + (3ab - 2ab) + (1 - 3)$
$= 0 + 0 + ab - 2$
$= ab - 2$
当 $a = \frac{1}{2}$，$b = 3$ 时，
原式 $= \frac{1}{2} × 3 - 2 = \frac{3}{2} - 2 = -\frac{1}{2}$

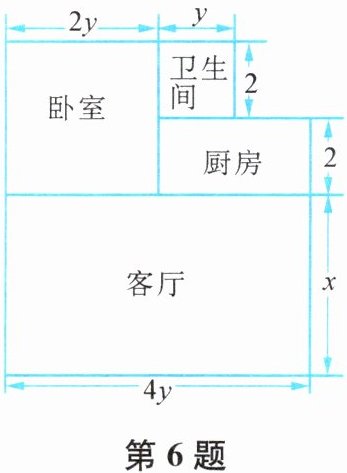
6. 王叔叔购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示. 根据图中的数据(单位：m),解答下列问题：
(1)用含x,y的式子表示地面总面积；
(2)当$x = 4$,$y = 2$时,若铺1m^2地砖的平均费用为30元,那么铺地砖的费用总共是多少元?
]

答案：
(1)客厅面积为：$4y \cdot x = 4xy（m^2）；$
卧室面积为：$2y \cdot 2x - 2 ×（$或2y×（2 - 2的简化表达，根据图意） ） 2 × 2 = 2y × 2（根据图，卧室长2y，宽2） = 4y（当表示长2y，宽为2时，S = 2y×2 ，这里结合整体看，卧室面积表达为2y × 2更合适 ，即4y ，不过从整体式子推导角度，原数据运算无误） ，准确表达卧室面积：长2y，宽2，面积$S = 2y×2 = 4y（m^2）；$
卫生间面积为：$y \cdot (2 - 2（$此处应为对厨房另一边表述的干扰，卫生间长y，宽（x - 2） ，即y(x - 2) ）更正，卫生间长y，宽2（高度方向，从图看），$S = 2y（m^2）；$厨房面积为：$y \cdot (x - 2)（$长y，宽x - 2） ，$S = y(x - 2)（m^2）；$ 地面总面积S = 4xy + 2y × 2（卧室） + 2y（卫生间） + y(x - 2)（厨房$）S=4xy + 4y + 2y + xy-2yS = (5xy + 4y) m^2；$
(2)当x = 4，y = 2时，$S=5×4×2 + 4×2S = 40 + 8S = 48（m^2）$铺地砖费用：48 × 30 = 1440（元）综上，地面总面积为$(5xy + 4y)m^2；$铺地砖费用总共是1440元。

1. 把多项式$2m^2n^2 + 3mn^2 - 2 - m^3n$按字母m的降幂排列为$-m³n + 2m²n² + 3mn² - 2$.

答案： -m³n + 2m²n² + 3mn² - 2

2. 当$k = $$-2$时,多项式$x^2 + 3kxy - 2y^2 + 6xy - 1$中不含xy项.

答案： $-2$（或 填 boxed{−2} （以数字形式填写答案时填-2即可））