第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
4. 火车站和机场都为旅客提供打包服务,如果长、宽、高分别为x,y,z的箱子按如图所示方式打包,则打包带的长度至少为( ).
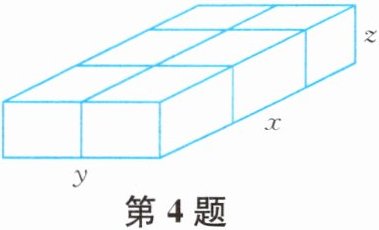

答案:
$2x + 4y + 6z$
5. 在弹性范围内,一根弹簧挂上物体后,弹簧长度与所挂物体质量的关系如表.
|所挂物体的质量/kg|1|2|3|4|5|
|弹簧总长度/cm|12|14|16|18|20|

根据表中信息回答:
(1)当挂上6kg物体时,弹簧总长度为
(2)未挂物体时,弹簧总长度为
(3)当挂上xkg物体时,弹簧总长度为
|所挂物体的质量/kg|1|2|3|4|5|
|弹簧总长度/cm|12|14|16|18|20|

根据表中信息回答:
(1)当挂上6kg物体时,弹簧总长度为
22
cm;(2)未挂物体时,弹簧总长度为
10
cm;(3)当挂上xkg物体时,弹簧总长度为
(2x + 10)
cm. (用含x的代数式表示)
答案:
(1)由表中数据可知,所挂物体质量每增加1kg,弹簧总长度增加2cm。
当挂上$5kg$物体时,弹簧总长度为$20cm$,所以当挂上$6kg$物体时,弹簧总长度为$20 + 2 = 22cm$。
(2)设未挂物体时,弹簧总长度为$b cm$,所挂物体质量为$x kg$时,弹簧总长度为$y cm$,$y$与$x$的关系式为$y = kx + b$。
取$x = 1$,$y = 12$和$x = 2$,$y = 14$代入关系式,得到方程组$\begin{cases}k + b = 12,\\2k + b = 14.\end{cases}$
用第二个方程减去第一个方程,得到$k = 2$,将$k = 2$代入第一个方程,得到$b = 10$。
所以未挂物体时,弹簧总长度为$10cm$。
(3)由
(2)可知$k = 2$,$b = 10$,所以当挂上$x kg$物体时,弹簧总长度为$(2x + 10)cm$。
故答案为:
(1)$22$;
(2)$10$;
(3)$(2x + 10)$。
(1)由表中数据可知,所挂物体质量每增加1kg,弹簧总长度增加2cm。
当挂上$5kg$物体时,弹簧总长度为$20cm$,所以当挂上$6kg$物体时,弹簧总长度为$20 + 2 = 22cm$。
(2)设未挂物体时,弹簧总长度为$b cm$,所挂物体质量为$x kg$时,弹簧总长度为$y cm$,$y$与$x$的关系式为$y = kx + b$。
取$x = 1$,$y = 12$和$x = 2$,$y = 14$代入关系式,得到方程组$\begin{cases}k + b = 12,\\2k + b = 14.\end{cases}$
用第二个方程减去第一个方程,得到$k = 2$,将$k = 2$代入第一个方程,得到$b = 10$。
所以未挂物体时,弹簧总长度为$10cm$。
(3)由
(2)可知$k = 2$,$b = 10$,所以当挂上$x kg$物体时,弹簧总长度为$(2x + 10)cm$。
故答案为:
(1)$22$;
(2)$10$;
(3)$(2x + 10)$。
6. 某施工队计划修xm长的环城公路,原计划每天修50m,因工期赶时间,实际每天修公路的速度比原计划提高了20%,
(1)这项工程原计划多少天完成;
(2)这项工程可提前多少天完成.
(1)这项工程原计划多少天完成;
(2)这项工程可提前多少天完成.
答案:
(1)原计划每天修50m,公路总长xm,根据工作时间=工作总量÷工作效率,原计划完成天数为:$\frac{x}{50}$天。
(2)实际每天修的速度比原计划提高20%,则实际每天修的长度为:$50×(1 + 20\%) = 50×1.2 = 60$m。实际完成天数为:$\frac{x}{60}$天。提前的天数=原计划天数 - 实际天数,即$\frac{x}{50}-\frac{x}{60}$,通分计算得:$\frac{6x}{300}-\frac{5x}{300}=\frac{x}{300}$天。
(1)$\frac{x}{50}$
(2)$\frac{x}{300}$
(1)原计划每天修50m,公路总长xm,根据工作时间=工作总量÷工作效率,原计划完成天数为:$\frac{x}{50}$天。
(2)实际每天修的速度比原计划提高20%,则实际每天修的长度为:$50×(1 + 20\%) = 50×1.2 = 60$m。实际完成天数为:$\frac{x}{60}$天。提前的天数=原计划天数 - 实际天数,即$\frac{x}{50}-\frac{x}{60}$,通分计算得:$\frac{6x}{300}-\frac{5x}{300}=\frac{x}{300}$天。
(1)$\frac{x}{50}$
(2)$\frac{x}{300}$
1. 用代数式表示:
(1)某影院针对某影片推出了特惠活动:票价每人30元,团体购票超过10人,所有人的票价可享受八折优惠,学校计划组织全体教师观看此影片. 若观影人数为a(a>10),则应付票价总额为
(2)某市出租车收费标准为:起步价7元,2km后每千米收费a元,则某人乘坐出租车8km需付费
(1)某影院针对某影片推出了特惠活动:票价每人30元,团体购票超过10人,所有人的票价可享受八折优惠,学校计划组织全体教师观看此影片. 若观影人数为a(a>10),则应付票价总额为
24a
元.(2)某市出租车收费标准为:起步价7元,2km后每千米收费a元,则某人乘坐出租车8km需付费
7 + 6a
元.
答案:
(1) 因为观影人数$a>10$,享受八折优惠,每人票价为$30×0.8 = 24$元,所以应付票价总额为$24a$元。
(2) 乘坐出租车$8km$,前$2km$收费$7$元,超过$2km$的部分为$8 - 2 = 6km$,这部分费用为$6a$元,所以总费用为$7 + 6a$元。
(1)$24a$
(2)$7 + 6a$
(1) 因为观影人数$a>10$,享受八折优惠,每人票价为$30×0.8 = 24$元,所以应付票价总额为$24a$元。
(2) 乘坐出租车$8km$,前$2km$收费$7$元,超过$2km$的部分为$8 - 2 = 6km$,这部分费用为$6a$元,所以总费用为$7 + 6a$元。
(1)$24a$
(2)$7 + 6a$
查看更多完整答案,请扫码查看


