第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
2. 某学校围棋社团组织成员进行比赛,规则如下:每两位选手都要进行比赛,决出胜负(没有平局),胜者得1分,负者得0分.在所有选手中,男选手有12人,女选手有9人.比赛结束后,经统计,女选手的总得分比男选手的总得分多70分.
(1)共进行了多少场比赛?
(2)男选手的总得分是多少分?
(1)共进行了多少场比赛?
(2)男选手的总得分是多少分?
答案:
(1) 总选手人数为 $12 + 9 = 21$ 人,每两位选手比赛一场,比赛场数为组合数 $C_{21}^2$。
$C_{21}^2 = \frac{21 × 20}{2} = 210$
故共进行了210场比赛。
(2) 设男选手总得分是 $x$ 分,则女选手总得分是 $x + 70$ 分。每场比赛产生1分,总积分等于比赛场数,即210分。
$x + (x + 70) = 210$
解得 $2x = 140$,$x = 70$。
(1) 210
(2) 70
(1) 总选手人数为 $12 + 9 = 21$ 人,每两位选手比赛一场,比赛场数为组合数 $C_{21}^2$。
$C_{21}^2 = \frac{21 × 20}{2} = 210$
故共进行了210场比赛。
(2) 设男选手总得分是 $x$ 分,则女选手总得分是 $x + 70$ 分。每场比赛产生1分,总积分等于比赛场数,即210分。
$x + (x + 70) = 210$
解得 $2x = 140$,$x = 70$。
(1) 210
(2) 70
3. 下表是某赛季篮球联赛部分球队的积分表:
|队名|比赛场次|胜场|负场|积分|
|前进|16|10|6|36|
|光明|16|9|7|34|
|远大|16|12|4|40|
|卫星|16|6|10|28|
|备注:积分= 胜场积分+负场积分|
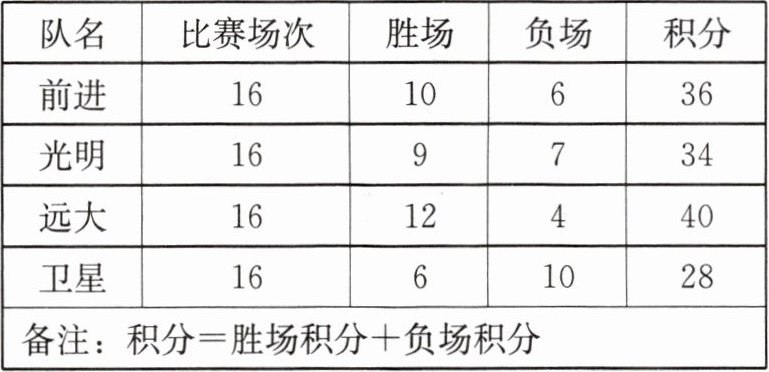
(1)求胜一场的积分和负一场的积分.
(2)某队说他们的总积分为45分,你认为可能吗?为什么?
(3)若某队的负场总积分是胜场总积分的正整数倍,胜一场奖励每名球员5000元,负一场奖励每名球员1000元,请问这支球队的每名球员所获奖金可能是多少元?
|队名|比赛场次|胜场|负场|积分|
|前进|16|10|6|36|
|光明|16|9|7|34|
|远大|16|12|4|40|
|卫星|16|6|10|28|
|备注:积分= 胜场积分+负场积分|

(1)求胜一场的积分和负一场的积分.
(2)某队说他们的总积分为45分,你认为可能吗?为什么?
(3)若某队的负场总积分是胜场总积分的正整数倍,胜一场奖励每名球员5000元,负一场奖励每名球员1000元,请问这支球队的每名球员所获奖金可能是多少元?
答案:
(1)设胜一场得$x$分,负一场得$y$分。根据前进队数据:$10x + 6y = 36$;光明队数据:$9x + 7y = 34$。联立方程组:
$\begin{cases}10x + 6y = 36 \\9x + 7y = 34\end{cases}$
解得$x = 3$,$y = 1$。
答:胜一场积3分,负一场积1分。
(2)设该队胜$m$场,负$n$场,则$\begin{cases}m + n = 16 \\ 3m + n = 45\end{cases}$,解得$m = 14.5$。胜场数必须为整数,故不可能。
(3)设胜$m$场,负$n$场,$n = 16 - m$。负场积分$n$,胜场积分$3m$,则$n = k \cdot 3m$($k$为正整数),即$16 - m = 3km$,$m = \frac{16}{3k + 1}$。
$m$为正整数,$3k + 1$为16的正因数:
$k=1$时,$3k + 1=4$,$m=4$,$n=12$,奖金$5000×4 + 1000×12=32000$元;
$k=5$时,$3k + 1=16$,$m=1$,$n=15$,奖金$5000×1 + 1000×15=20000$元。
答:每名球员所获奖金可能是20000元或32000元。
(1)设胜一场得$x$分,负一场得$y$分。根据前进队数据:$10x + 6y = 36$;光明队数据:$9x + 7y = 34$。联立方程组:
$\begin{cases}10x + 6y = 36 \\9x + 7y = 34\end{cases}$
解得$x = 3$,$y = 1$。
答:胜一场积3分,负一场积1分。
(2)设该队胜$m$场,负$n$场,则$\begin{cases}m + n = 16 \\ 3m + n = 45\end{cases}$,解得$m = 14.5$。胜场数必须为整数,故不可能。
(3)设胜$m$场,负$n$场,$n = 16 - m$。负场积分$n$,胜场积分$3m$,则$n = k \cdot 3m$($k$为正整数),即$16 - m = 3km$,$m = \frac{16}{3k + 1}$。
$m$为正整数,$3k + 1$为16的正因数:
$k=1$时,$3k + 1=4$,$m=4$,$n=12$,奖金$5000×4 + 1000×12=32000$元;
$k=5$时,$3k + 1=16$,$m=1$,$n=15$,奖金$5000×1 + 1000×15=20000$元。
答:每名球员所获奖金可能是20000元或32000元。
查看更多完整答案,请扫码查看


