7. 在点子图中选一个点D(只能选在点子上),使点A、B、C、D正好围成一个梯形,共有4种围法,请你在点子图中画出这些围法。


答案:
本题可根据梯形的定义,结合点子图来确定点$D$的位置。
梯形是指一组对边平行而另一组对边不平行的四边形。已知$A$、$B$、$C$三点,$AB$与$BC$不平行,$AB$与$AC$不平行,$BC$与$AC$不平行,且$BC$为水平线段。
围法一
在$A$点正上方且与$A$点在同一列的点子处取点$D_1$,此时$AD_1$与$BC$平行,$AB$与$CD_1$不平行,满足梯形的定义,即图①的情况。
围法二
在$C$点正上方且与$C$点在同一列的点子处取点$D_2$,此时$CD_2$与$AB$平行,$BC$与$AD_2$不平行,满足梯形的定义,即图②的情况。
围法三
在$B$点左上方,使得$BD_3$与$AC$平行的点子处取点$D_3$,此时$BD_3$与$AC$平行,$AB$与$CD_3$不平行,满足梯形的定义,即图③的情况。
围法四
在$B$点右上方,使得$BD_4$与$AC$平行的点子处取点$D_4$,此时$BD_4$与$AC$平行,$AB$与$CD_4$不平行,满足梯形的定义,即图④的情况。
综上,按照上述四种情况在点子图中画出点$D$的位置即可。
梯形是指一组对边平行而另一组对边不平行的四边形。已知$A$、$B$、$C$三点,$AB$与$BC$不平行,$AB$与$AC$不平行,$BC$与$AC$不平行,且$BC$为水平线段。
围法一
在$A$点正上方且与$A$点在同一列的点子处取点$D_1$,此时$AD_1$与$BC$平行,$AB$与$CD_1$不平行,满足梯形的定义,即图①的情况。
围法二
在$C$点正上方且与$C$点在同一列的点子处取点$D_2$,此时$CD_2$与$AB$平行,$BC$与$AD_2$不平行,满足梯形的定义,即图②的情况。
围法三
在$B$点左上方,使得$BD_3$与$AC$平行的点子处取点$D_3$,此时$BD_3$与$AC$平行,$AB$与$CD_3$不平行,满足梯形的定义,即图③的情况。
围法四
在$B$点右上方,使得$BD_4$与$AC$平行的点子处取点$D_4$,此时$BD_4$与$AC$平行,$AB$与$CD_4$不平行,满足梯形的定义,即图④的情况。
综上,按照上述四种情况在点子图中画出点$D$的位置即可。
(1)数学课本封面的上下两条边互相(
平行
), 左右两条边互相(平行
), 相邻的两条边互相(垂直
)。
答案:
答题卡:
(1)
数学课本封面的上下两条边互相平行,
左右两条边互相平行,
相邻的两条边互相垂直。
(1)
数学课本封面的上下两条边互相平行,
左右两条边互相平行,
相邻的两条边互相垂直。
(2)小明用铁丝做了一个平行四边形的框架,一组邻边分别是6厘米和4厘米,至少需要用(
20
)厘米的铁丝。
答案:
答题卡:
(2)
解:平行四边形周长计算公式为 P = 2(a + b),其中a和b为邻边长度。
代入a = 6厘米,b = 4厘米,得:
P = 2 × (6 + 4) = 20(厘米)
答:至少需要用20厘米的铁丝。
(2)
解:平行四边形周长计算公式为 P = 2(a + b),其中a和b为邻边长度。
代入a = 6厘米,b = 4厘米,得:
P = 2 × (6 + 4) = 20(厘米)
答:至少需要用20厘米的铁丝。
(3)两条直线互相垂直,这两条直线相交的角一定是(
B
)。
答案:
B(假设B选项为直角)
(4)在右图的平行四边形中,线段CD对应的高是线段(
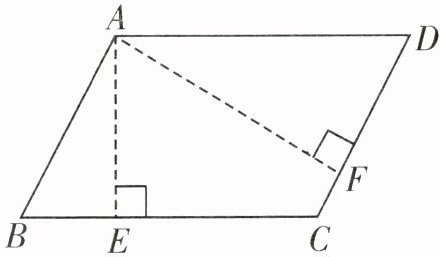
AF
)。
答案:
AF
(1)一个四边形的两组对边分别平行,这个四边形一定是(
① 正方形 ② 长方形 ③ 平行四边形
C
)。① 正方形 ② 长方形 ③ 平行四边形
答案:
C
(2)学校的伸缩门利用了平行四边形的(
① 不稳定性 ② 稳定性 ③ 牢固性
A
)。① 不稳定性 ② 稳定性 ③ 牢固性
答案:
A
查看更多完整答案,请扫码查看


