《2025年新编基础训练九年级物理上册通用版Y》

- 功
概念:作用在物体上的力,使物体在①上移动一段距离,就说这个力对物体做了机械功,简称做了功
定义式:$W = Fs$
单位:$J$,$1J = 1N\cdot m$
- 功率
概念:把做功的多少与所用时间的比叫做功率
定义式:②
导出式:$P = Fv$;单位:$W$,$1kW = 10^{3}W$
- 机械效率
概念:把有用功$W_{有用}与总功W_{总}$的比值叫做机械效率
定义式:$\eta=\frac{W_{有用}}{W_{总}}×100\%$
相关公式:$W_{总}= W_{有用}+W_{额外}$
- 动能和势能
动能
概念:物体由于③具有的能
影响因素:④和速度
势能
重力势能
概念:被举高的物体具有的能
影响因素:质量和被举高的高度
弹性势能
概念:物体发生弹性形变而具有的能
影响因素:弹簧的弹性和弹簧的形变量
动能和势能可相互⑤
①力的方向 ②$P=\frac{W}{t}$ ③运动 ④质量 ⑤转化

答案： ①力的方向 ②$P=\frac{W}{t}$ ③运动 ④质量 ⑤转化

1. 如图所示,图甲中人将桶推到仓库中,桶在人的推力的作用下移动到了仓库中。而图乙中举重运动员举着杠铃不动,杠铃在运动员的举力作用下没有移动。在物理学中,我们说图甲中的人对桶做了(选填“做了”或“没有做”)功,举重运动员对杠铃没有做(选填“做了”或“没有做”)功。由此可知,做功的两个必要条件是作用在物体上的力和物体在力的方向上移动的距离。

答案： 做了 没有做 力 距离

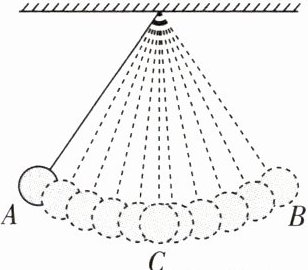
2. 如图所示,将小球拉到点$A$处,然后由静止开始释放。由$A到C$的过程中,小球的高度降低,速度增大,即小球的重力势能减小,动能增大,重力势能转化为动能;由$C至B$的过程中,小球的速度减小,高度增大,即小球的动能减小,重力势能增大,动能转化为重力势能。由此可知,摆球的动能与势能是可以相互转化的。

答案： 重力势 动 重力势 动 动 重力势 动 重力势 相互转化