第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 填一填。
(1) 把一个圆沿半径平均分成若干份,然后拼成一个近似长方形,长方形的长近似于(
(2) 用一根长为4m的绳子系在树上画一个最大的圆(不计树粗和系口处绳子损耗),这个圆的半径是(
(3) 圆的半径扩大到原来的4倍,周长扩大到原来的(
(4) 圆的半径为8dm,如果半径减少2dm,周长减少(
(1) 把一个圆沿半径平均分成若干份,然后拼成一个近似长方形,长方形的长近似于(
圆周长的一半
),宽近似于(圆的半径
),从而得到圆的面积计算公式($S=\pi r^{2}$
)。(2) 用一根长为4m的绳子系在树上画一个最大的圆(不计树粗和系口处绳子损耗),这个圆的半径是(
4
)m,周长是(25.12
)m,面积是(50.24
)$m^2。$(3) 圆的半径扩大到原来的4倍,周长扩大到原来的(
4
)倍,面积扩大到原来的(16
)倍。(4) 圆的半径为8dm,如果半径减少2dm,周长减少(
12.56
)dm,面积减少(87.92
)$dm^2。$
答案:
1.
(1)圆周长的一半 圆的半径 $ S=\pi r^{2} $
(2)4 25.12 50.24
(3)4 16
(4)12.56 87.92
(1)圆周长的一半 圆的半径 $ S=\pi r^{2} $
(2)4 25.12 50.24
(3)4 16
(4)12.56 87.92
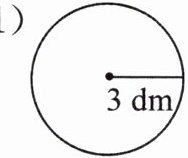
2. 求出下面圆的面积。
(1)
(2)
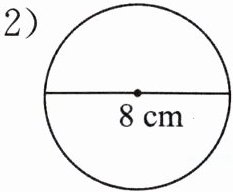
(1)

(2)

答案:
2.
(1)$ 3.14× 3^{2}=28.26(dm^{2}) $
(2)$ 3.14× (8÷ 2)^{2}=50.24(cm^{2}) $
(1)$ 3.14× 3^{2}=28.26(dm^{2}) $
(2)$ 3.14× (8÷ 2)^{2}=50.24(cm^{2}) $
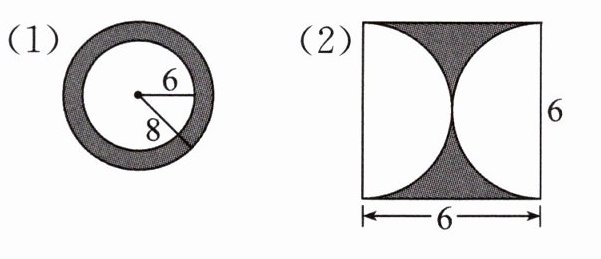
3. 求下列图形中阴影部分的面积。(单位:dm)
(1)
(2)
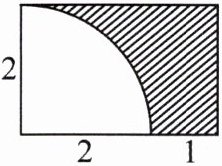
(3)
(1)
(2)

(3)

答案:
3.
(1)$ 3.14× (8^{2}-6^{2})=87.92(dm^{2}) $
(2)$ 6× 6-3.14× (6÷ 2)^{2}=7.74(dm^{2}) $
(3)$ (2+1)× 2-3.14× 2^{2}× \frac{1}{4}=2.86(dm^{2}) $
(1)$ 3.14× (8^{2}-6^{2})=87.92(dm^{2}) $
(2)$ 6× 6-3.14× (6÷ 2)^{2}=7.74(dm^{2}) $
(3)$ (2+1)× 2-3.14× 2^{2}× \frac{1}{4}=2.86(dm^{2}) $
4. 公园里有一个圆形花坛,直径是5m,在它周围有一条宽为1m的圆环形鹅卵石小路,小路的面积是多少平方米?
答案:
$ 5÷ 2=2.5(m) $ $ 2.5+1=3.5(m) $
$ 3.14× (3.5^{2}-2.5^{2})=18.84(m^{2}) $
$ 3.14× (3.5^{2}-2.5^{2})=18.84(m^{2}) $
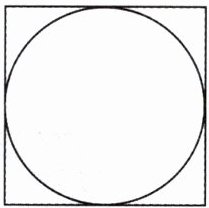
5. 如图,正方形的边长是28cm,圆的直径也是28cm,正方形与圆之间的面积有多少平方厘米?

答案:
$ 28× 28-3.14× (\frac{28}{2})^{2}=168.56(cm^{2}) $
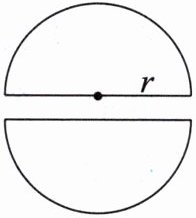
6. 如图,某小区有两个半圆形的花坛,它们的周长都是154.2m,这两个花坛占地总面积是多少平方米?

答案:
$ 3.14× 2r÷ 2+2r=154.2 $ $ r=30\ m $
$ 3.14× 30^{2}=2826(m^{2}) $
$ 3.14× 30^{2}=2826(m^{2}) $
查看更多完整答案,请扫码查看


