《2025年新编基础训练七年级数学上册人教版》

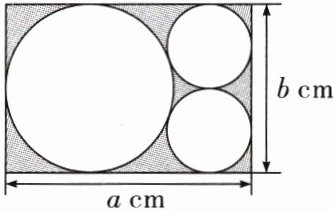
10. (20 分)剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术.在校园文化艺术节的剪纸展示中,小华在一张长为$a$cm、宽为$b$cm 的长方形纸片上,剪掉一个大圆和两个半径相等的小圆(如图所示).
(1) 列出表示剩余纸片(图中阴影部分)面积的代数式(结果可不化简)；
(2) 当$a = 6$,$b = 4$时,求阴影部分的面积($\pi取3.14$).

答案：
(1)从图中看出:大圆半径为$\frac{b}{2}$cm,小圆半径为$\frac{b}{4}$cm,所以阴影部分面积为长方形面积-大圆面积-2个小圆面积$=ab-\pi(\frac{b}{2})^{2}-\pi(\frac{b}{4})^{2}×2=ab-\frac{\pi b^{2}}{4}-\frac{\pi b^{2}}{8}(cm^{2})$.
(2)因为$a=6$,$b=4$,$\pi$取3.14,所以阴影部分面积$=ab-\frac{\pi b^{2}}{4}-\frac{\pi b^{2}}{8}\approx6×4-\frac{3.14×4^{2}}{4}-\frac{3.14×4^{2}}{8}=5.16(cm^{2})$.

11. (20 分)在探究“水沸腾时温度变化特点”的实验中,发现在水沸腾前,水的温度$y$(℃)与加热时间$x$(min)之间成一定的关系,下表记录了实验中水的温度$y$(℃)和加热时间$x$(min)变化的部分数据.
\begin{tabular}{|c|c|c|c|c|c|}
\hline 加热时间$x$/min & $5$ & $10$ & $15$ & $20$ & $25$ \\
\hline 温度$y$/℃ & $25$ & $40$ & $55$ & $70$ & $85$ \\
\hline
\end{tabular}\\
\hline


(1) 用式子表示水在沸腾前,水的温度$y$(℃)与加热时间$x$(min)之间的关系；
(2) 求当加热$18$min 时水的温度.

答案：
(1)由表格数据知y与x的关系可用式子$y=3x+10$表示.
(2)当$x=18$时,$y=3×18+10=64(^{\circ}C)$,所以加热18 min时水的温度是$64^{\circ}C$.