《2025年新编基础训练七年级数学上册人教版》

5. 某市三年前的人均年收入为$m$元,预计今年的人均年收入比三年前的2倍多500元,则今年的人均年收入将达到______元(用含$m$的代数式表示)。

答案： (2m+500)

6. (开放性题)请你结合自身生活实际,设计具体情境,解释下列代数式的意义：
(1)$(1 - 20\%)x$；(2)$\frac{30}{m}$；(3)$(1 + 10\%)x$；(4)$\frac{3m + 2n}{5}$。

答案： 解:(答案不唯一)
(1)小明家二月份用电x千瓦时,三月份用电量减少20%,则三月份用电(1-20%)x千瓦时.
(2)汽车每小时行驶m km,行驶30 km所用时间为$\frac{30}{m}$h.
(3)某款价格为x元的钢笔加价10%后的售价是(1+10%)x元.
(4)巧克力糖每千克m元,奶油糖每千克n元,用3 kg巧克力糖和2 kg奶油糖混合成5 kg什锦糖,则这样得到的什锦糖每千克的平均价格为$\frac{3m+2n}{5}$元.

7. 下列关于代数式“$3x + 2y$”的意义叙述不正确的有( )
①$x$的3倍与$y$的2倍的和；②小明跑步的速度为$x$ km/h,步行的速度为$y$ km/h,则小明跑步3 h后步行2 h,共走了$(3x + 2y)$km；③某小商品以每个3元的价格卖出了$x$个,又以每个2元的价格卖出了$y$个,则共卖了$(3x + 2y)$元。

A.3个
B.2个
C.1个
D.0个

答案： D

8. 填空：
(1)三个连续整数,中间一个偶数是$2n$,则第一个和第三个整数分别是______,______；
(2)三个连续奇数,中间一个是$n$,则它前一个和后一个奇数分别是______,______。

答案：
(1)2n-1 2n+1
(2)n-2 n+2

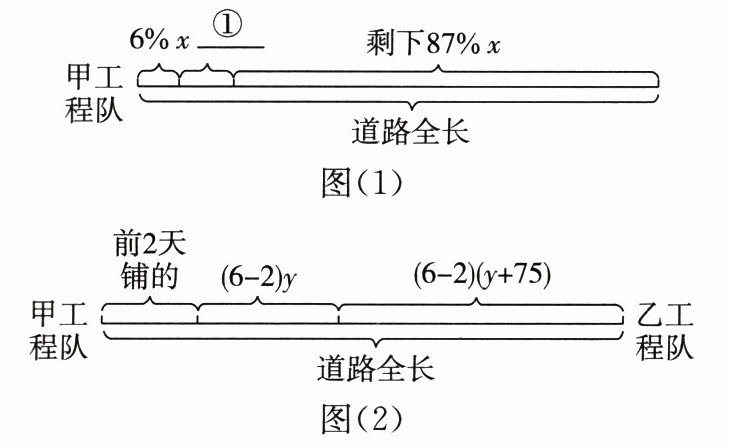
9. 为建设文明城市,某社区计划将社区内一条东西走向的水泥道路铺设成沥青道路,俗称“白改黑”。甲工程队负责这条道路的铺设,他们从西头开始铺,计划6天内完成。第一天铺了全长的6%,第二天铺的道路比第一天的2倍少60 m,此时还剩下全长的87%没铺。
(1)若用图(1)表示前两天甲工程队的进度情况,请写出图(1)中①处应填写的内容,并写出图中$x$所表示的实际意义；
(2)为按时完成铺路任务,从第三天开始,甲工程队加快速度,同时乙工程队加入铺路,从东头开始铺。两队的进展情况如图(2)所示,已知$y$表示甲工程队加快速度后每天铺路的长度,请根据图(2)写出$(6 - 2)y$,$y + 75$,$(6 - 2)(y + 75)$分别表示的意义。

答案： 解:
(1)①处应填写$2×6\% x-60$.x表示道路的全长.
(2)(6-2)y表示甲工程队加速后4天铺路的长度；y+75表示乙工程队每天铺路的长度；(6-2)(y+75)表示乙工程队4天铺路的总长度.

10. 说出下列代数式的意义：
(1)如果一件商品原价为$a$元,那么$a(1 + x\%)$表示什么？
(2)若苹果每千克$p$元,橘子每千克$q$元,则代数式$50 - (6p + 4q)$表示什么？

答案： 解:
(1)$a(1+x\%)$表示该商品价格上涨x%后的价格.
(2)代数式50-(6p+4q)表示用50元买6 kg苹果和4 kg橘子剩余的钱.