《2025年新编基础训练七年级数学上册人教版》

3. 下面算法正确的是( )

A.$(-5) + 9 = -(9 - 5)$
B.$7 - (-10) = 7 - 10$
C.$(-5)×0 = -5$
D.$(-8)÷(-4) = 8÷4$

答案： D

4. 已知 $a$,$b$ 都是实数,若 $(a + 2)^2 + |b - 1| = 0$,则 $(a + b)^{2023}$ 的值是( )

A.-2 023
B.-1
C.1
D.2 023

答案： B

5. (2024·上海中考)科学家研发了一种新的蓝光唱片,一张蓝光唱片的容量约为 $2×10^5$ GB,一张普通唱片的容量约为 25 GB,则蓝光唱片的容量是普通唱片的_____倍。(用科学记数法表示)

答案： 8×10³

6. (整体代入)若 $m$,$n$ 互为相反数,$p$,$q$ 互为倒数,则 $-2023m + \frac{3}{pq} - 2023n$ 的值是_____。

答案： 3

7. (分类讨论)已知有理数 $a$,$b$,$c$ 满足 $|a + b + c| = a + b - c$,且 $c ≠ 0$,则 $|a + b - c + 2| - |c - 10| = $ _____。

答案： -8

8. 有 2 023 个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和。如果第一个数是 0,第二个数是 1,那么这 2 023 个数的和是_____。

答案： 0

9. (30 分)计算：
(1)$-48×(\frac{1}{6} - \frac{5}{12} + \frac{3}{8}) - 6÷(\frac{1}{3} - \frac{1}{2})$；
(2)$-2^3×(-3) + (-1)^{2023} + 4^2÷(-2)^3 - |-3^2|$；
(3)$99×(-99\frac{98}{99})$。

答案： 解:
(1)-48×(1/6 - 5/12 + 3/8)-6÷(1/3 - 1/2)=-48×1/6 + 48×5/12 - 48×3/8 -6÷(-1/6)=-8+20-18-6×(-6)=-8+20-18+36=30.
(2)-2³×(-3)+(-1)²⁰²³+4²÷(-2)³ -|-3²|=-8×(-3)+(-1)+16÷(-8)-|-9|=24-1+(-2)-9=24-1-2-9=12.
(3)99×(-99 98/99)=99×(-100+1/99)=99×(-100)+99×1/99=-9900+1=-9899.

10. (30 分)(数学文化)概念感知：第十四届国际数学教育大会(ICME - 14)会徽如图(1)所示,该主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数 3745。八进制是以 8 作为进位基数的数字系统,有 0～7 共 8 个基本数字,八进制数 3745 换算成十进制数是 $3×8^3 + 7×8^2 + 4×8^1 + 5×8^0 = 2021$,表示 $ICME - 14$ 的举办年份。
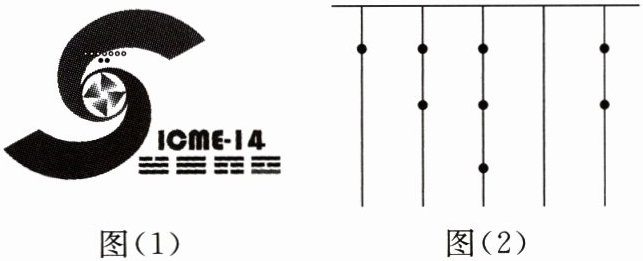
(1)请把八进制数 2163 换算成十进制数；
(2)应用拓展：据我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量。如图(2)所示,一位妇女在从右到左依次排列的绳子上打结来记录自己采集到的野果数量,满六进一,她一共采集到的野果数量为多少？

答案： 解:
(1)2×8³+1×8²+6×8¹+3×8⁰=1024+64+48+3=1139.
(2)1×6⁴+2×6³+3×6²+0×6¹+2×6⁰=1296+432+108+2=1838.即她一共采集到的野果数量为1838.