第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
2. 下列变形中正确使用加法交换律的是( )
A.$(-5) + (-8) = -(5 + 8)$
B.$(-7) + 11 = 7 + (-11)$
C.$(-3) + (-4) = (-4) + (-3)$
D.$4 + 6 = (-4) + (-6)$
A.$(-5) + (-8) = -(5 + 8)$
B.$(-7) + 11 = 7 + (-11)$
C.$(-3) + (-4) = (-4) + (-3)$
D.$4 + 6 = (-4) + (-6)$
答案:
C
3. 已知 $|m| = 14$,$|n| = 23$,且 $m + n > 0$,则 $m - n = $ ______。
答案:
-9或-37
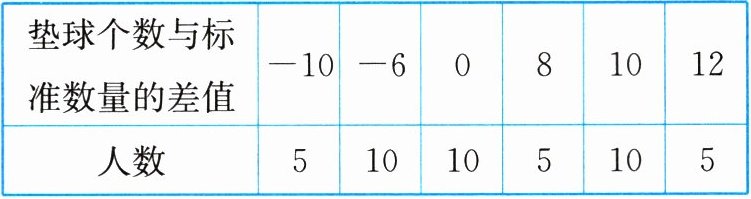
4. 某中学积极倡导阳光体育运动,开展了排球垫球比赛,下表为七年级某班 45 人参加排球垫球比赛的情况,标准为每人垫球 25 个。
|垫球个数与标准数量的差值| -10 | -6 | 0 | 8 | 10 | 12 |
|人数| 5 | 10 | 10 | 5 | 10 | 5 |
(1)这个班 45 人平均每人垫球多少个?
(2)规定垫球达到标准数量记 0 分,超过标准数量,每多垫 1 个加 2 分;未达到标准数量,每少垫 1 个扣 1 分,则这个班垫球总共获得多少分?
|垫球个数与标准数量的差值| -10 | -6 | 0 | 8 | 10 | 12 |
|人数| 5 | 10 | 10 | 5 | 10 | 5 |

(1)这个班 45 人平均每人垫球多少个?
(2)规定垫球达到标准数量记 0 分,超过标准数量,每多垫 1 个加 2 分;未达到标准数量,每少垫 1 个扣 1 分,则这个班垫球总共获得多少分?
答案:
解:
(1)-10×5+(-6)×10+0×10+8×5+10×10+12×5=-50-60+0+40+100+60=90(个),(25×45+90)÷45=1215÷45=27(个).答:这个班45人平均每人垫球27个.
(2)2×(8×5+10×10+12×5)-1×(| -10|×5+| -6|×10)=290(分).答:这个班垫球总共获得290分.
(1)-10×5+(-6)×10+0×10+8×5+10×10+12×5=-50-60+0+40+100+60=90(个),(25×45+90)÷45=1215÷45=27(个).答:这个班45人平均每人垫球27个.
(2)2×(8×5+10×10+12×5)-1×(| -10|×5+| -6|×10)=290(分).答:这个班垫球总共获得290分.
5. 已知一个数的相反数是 $2\frac{2}{3}$,另一个数的绝对值是 $2\frac{1}{4}$,则这两个数的积为_____。
答案:
6或-6
6. (新定义)我们规定 $m※n = \begin{cases} -mn(m \geq n) \\ m ÷ n(m < n) \end{cases} $,则 $(-\frac{1}{3})※(-6)※5$ 等于( )
A.-1
B.1
C.$-\frac{2}{5}$
D.$\frac{2}{5}$
A.-1
B.1
C.$-\frac{2}{5}$
D.$\frac{2}{5}$
答案:
C
7. (分类讨论)小慧同学在计算 $a + b$,$a - b$,$ab$,$\frac{a}{b}$ 的值时,发现有三个结果恰好相同,其中 $a$ 和 $b$ 都是有理数,则 $(8a)^{b + 2} = $ _____。
答案:
±4
8. (2024·安徽中考)据统计,2023 年我国新能源汽车产量超过 944 万辆,其中 944 万用科学记数法表示为( )
A.$0.944×10^7$
B.$9.44×10^6$
C.$9.44×10^7$
D.$94.4×10^6$
A.$0.944×10^7$
B.$9.44×10^6$
C.$9.44×10^7$
D.$94.4×10^6$
答案:
B
9. 将 30 974 四舍五入,得到近似数 3.10 万,则近似数精确到_____位。
答案:
百
10. 近似数 1.70 的准确值 $a$ 的取值范围是______。
答案:
1.695≤a<1.705
1. 如图所示,比数轴上点 A 表示的数大 3 的数是( )
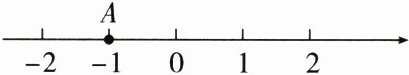
A.-1
B.0
C.1
D.2
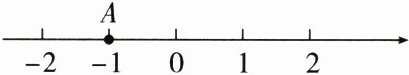
A.-1
B.0
C.1
D.2
答案:
D
2. (2024·长沙中考)“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器。“玉兔号”月球车能够耐受月球表面的最低温度是 -180℃,最高温度是 150℃,则它能够耐受的温差是( )
A.-180℃
B.150℃
C.30℃
D.330℃
A.-180℃
B.150℃
C.30℃
D.330℃
答案:
D
查看更多完整答案,请扫码查看


