《2025年新编基础训练七年级数学上册人教版》

4. (2024·淮北)下列各组数中,相等的一组是( )

A.$ -(-1) $ 与 $ -|-1| $
B.$ -3^{2} $ 与 $ (-3)^{2} $
C.$ (-4)^{3} $ 与 $ -4^{3} $
D.$ \frac{2^{2}}{3} $ 与 $ \left(\frac{2}{3}\right)^{2} $

答案： C

5. 比较大小：$ -\left|-\frac{8}{3}\right| $______$ -\left(\frac{3}{2}\right)^{2} $(选填“$ ＞ $”“$ ＜ $”或“$ = $”).

答案： ＜

【例 3】有一种纸的厚度为 $ 0.1 $ mm,若拿两张重叠在一起,将它对折 $ 1 $ 次后,厚度为 $ 2^{2} × 0.1 $ mm.
(1)对折 $ 2 $ 次后,厚度为多少毫米？
(2)对折 $ 6 $ 次后,厚度为多少毫米？

答案： 解:
(1)$2×2^{2}×0.1=0.8(mm).$
答:对折2次后,厚度为0.8 mm.
(2)$2^{5}×2^{2}×0.1=12.8(mm).$
答:对折6次后,厚度为12.8 mm.

根据对折规律,每对折一次,厚度是前一次的 $ 2 $ 倍,所以对折 $ n $ 次后,厚度为对折前的 $ 2^{n} $ 倍.

答案： 答：设纸张初始厚度为 $h$，
对折 $n$ 次后，厚度为 $h × 2^{n}$。

6. 一根 $ 1 $ m 长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,剪九次后剩下的绳子的长度为( )

A.$ \left(\frac{1}{2}\right)^{6} $ m
B.$ \left(\frac{1}{2}\right)^{7} $ m
C.$ \left(\frac{1}{2}\right)^{8} $ m
D.$ \left(\frac{1}{2}\right)^{9} $ m

答案： D

7. 有一块面积为 $ 64 $ $ m^{2} $ 的正方形纸片,第一次剪掉一半,第二次剪掉剩下纸片的一半,如此继续剪下去,剪六次后剩下的纸片的面积是多少平方米？

答案： 解:$64×(\frac {1}{2})^{6}=64×\frac {1}{64}=1(m^{2}).$
答:剪六次后,剩下的纸片的面积是$1m^{2}.$

1. 计算 $ \frac{\overbrace{2 × 2 × … × 2}^{m 个 2}}{\underbrace{3 + 3 + … + 3}_{n 个 3}} $ 的值为( )


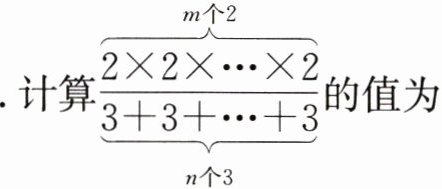
A.$ \frac{2m}{3^{n}} $
B.$ \frac{2^{m}}{3n} $
C.$ \frac{2m}{n^{3}} $
D.$ \frac{m^{2}}{3n} $

答案： B

2. 甲、乙、丙、丁 $ 4 $ 位同学,在学了有理数的乘方之后,发表了以下见解,观点正确的有( )
甲：$ 2^{5} $ 是 $ 2 $ 个 $ 5 $ 相加；
乙：$ -\left(\frac{3}{4}\right)^{3} $ 与 $ \left(-\frac{3}{4}\right)^{3} $ 有不同的结果；
丙：$ (-3)^{4} $ 的底数是 $ -3 $,指数是 $ 4 $；
丁：$ n^{4} $ 是 $ n $ 个 $ 4 $ 相乘.

A.$ 0 $ 个
B.$ 1 $ 个
C.$ 2 $ 个
D.$ 3 $ 个

答案： B

3. $ (-5)^{3} $ 的意义是______,$ -5^{3} $ 的意义是______.

答案： 3个-5相乘 5的3次方的相反数

4. 已知有理数 $ x $,$ y $,若 $ |x| = 3 $,$ |y| = 2 $,且 $ x ＜ 0 ＜ y $,则 $ x^{y} = $______.

答案： 9

5. 填空：
(1)$ \left(-\frac{1}{3}\right)^{2} = $______；
(2)$ (-7)^{3} = $______；
(3)$ (-0.2)^{3} = $______；
(4)$ -2^{4} = $______；
(5)$ -(-3)^{3} = $______.

答案：
(1)$\frac {1}{9}$
(2)-343
(3)-0.008
(4)-16
(5)27

6. 水葫芦是一种水生漂浮植物,有着惊人的繁殖能力. 据研究表明：适量的水葫芦生长对水质的净化是有利的. 若在适宜的条件下,$ 1 $ 株水葫芦每 $ 5 $ 天就能繁殖 $ 1 $ 株(不考虑死亡、被打捞等其他因素).
(1)假设湖面上现有 $ 1 $ 株水葫芦,填写下表；
| 天数 | $ 5 $ | $ 10 $ | $ 15 $ | …$ $ | $ 25 $ | …$ $ | $ 5n $ |
| 总株数 | $ 2 $ | $ 4 $ | | …$ $ | | …$ $ | |

(2)假定某个水域的水葫芦维持在 $ 1280 $ 株以内对水质净化有益. 若现有 $ 10 $ 株水葫芦,请你计算,按照上述生长速度,多少天时该水域将有 $ 1280 $ 株水葫芦？

答案： 解:
(1)8 32 $2^{n}$
(2)根据题意,得$10×2^{n}=1280,$
解得$n=7,7×5=35$(天).
答:按照上述生长速度,35天时该水域将有1280株水葫芦.