第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
1. 计算$3 - 5$等于( )
A.$2$
B.$-2$
C.$8$
D.$-8$
A.$2$
B.$-2$
C.$8$
D.$-8$
答案:
B
2. (2024·安徽)计算$1-(-3)$的结果是( )
A.$-2$
B.$4$
C.$-4$
D.$2$
A.$-2$
B.$4$
C.$-4$
D.$2$
答案:
B
3. 下列说法正确的是( )
A.减去一个数等于加上这个数
B.两个相反数相减得$0$
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
A.减去一个数等于加上这个数
B.两个相反数相减得$0$
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
答案:
D
4. $|a| = 2$,$|b| = 5$,且$a < 0$,$b > 0$,则$a - b$的值为______.
答案:
-7
5. 珍珍同学在计算“$8 - 5\dfrac{1}{2}-\dfrac{1}{2}$”时,做法如下:
$8 - 5\dfrac{1}{2}-\dfrac{1}{2}= 8+(-5\dfrac{1}{2}-\dfrac{1}{2})$(第①步)
$=8+(-5)$(第②步)
$=3$.(第③步)
(1)珍珍同学对照答案后发现计算结果是错误的,则她开始出错的步骤是第______(填序号)步;
(2)求出本题正确的计算过程.
$8 - 5\dfrac{1}{2}-\dfrac{1}{2}= 8+(-5\dfrac{1}{2}-\dfrac{1}{2})$(第①步)
$=8+(-5)$(第②步)
$=3$.(第③步)
(1)珍珍同学对照答案后发现计算结果是错误的,则她开始出错的步骤是第______(填序号)步;
(2)求出本题正确的计算过程.
答案:
(1)②
(2)$8-5\frac{1}{2}-\frac{1}{2}$
$=8+(-5\frac{1}{2}-\frac{1}{2})$
$=8+(-6)$
$=8-6$
$=2$.
(1)②
(2)$8-5\frac{1}{2}-\frac{1}{2}$
$=8+(-5\frac{1}{2}-\frac{1}{2})$
$=8+(-6)$
$=8-6$
$=2$.
6. 计算:
(1)$0-(-6.1)$;(2)$-|-\dfrac{3}{2}|-(-5\dfrac{1}{2})$;
(3)$(-32)-(-27)-(-72)$.
(1)$0-(-6.1)$;(2)$-|-\dfrac{3}{2}|-(-5\dfrac{1}{2})$;
(3)$(-32)-(-27)-(-72)$.
答案:
(1)0-(-6.1)=0+6.1=6.1.
(2)$-|-\frac{3}{2}|-(-5\frac{1}{2})=-\frac{3}{2}+5\frac{1}{2}=4$.
(3)(-32)-(-27)-(-72)=(-32)+27+72
=-5+72=67.
(1)0-(-6.1)=0+6.1=6.1.
(2)$-|-\frac{3}{2}|-(-5\frac{1}{2})=-\frac{3}{2}+5\frac{1}{2}=4$.
(3)(-32)-(-27)-(-72)=(-32)+27+72
=-5+72=67.
7. (1)已知甲数是$4$的相反数,乙数比甲数的相反数大$3$,则乙数比甲数大多少?
(2)某天,月球表面的温度中午是$101^{\circ}C$,半夜是$-153^{\circ}C$,则中午比半夜温度高多少?
(2)某天,月球表面的温度中午是$101^{\circ}C$,半夜是$-153^{\circ}C$,则中午比半夜温度高多少?
答案:
(1)由题意,得甲数为-4,乙数为4+3=7,
所以7-(-4)=7+4=11.
故乙数比甲数大11.
(2)101-(-153)=101+153=254.
故中午比半夜温度高$254^{\circ}C$.
(1)由题意,得甲数为-4,乙数为4+3=7,
所以7-(-4)=7+4=11.
故乙数比甲数大11.
(2)101-(-153)=101+153=254.
故中午比半夜温度高$254^{\circ}C$.
8. 有理数$m$,$n$在数轴上的对应点如图所示,则$m - n$是( )
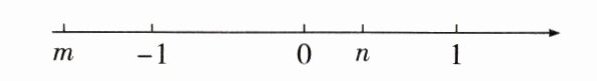
A.正数
B.负数
C.$0$
D.无法确定
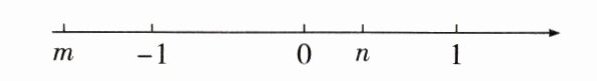
A.正数
B.负数
C.$0$
D.无法确定
答案:
B
9. 在高速公路上开车时,父亲注意到汽车的里程表显示为$15951$km,这种向前和向后读是一样的数称为回文数.$1$h后,里程表显示为下一个稍大一点的回文数,在这期间汽车行驶了______km.
答案:
110
10. 数轴上线段的长度可以由线段端点表示的数进行减法运算得到,如图所示,线段$AB = 0 - (-1)= 1$,线段$BC = 2 - 0 = 2$,线段$AC = 2 - (-1)= 3$.

(1)数轴上点$M$,$N表示的数分别为-9和1$,则线段$MN= $______;
(2)数轴上点$E$,$F表示的数分别为-6和-3$,则线段$EF= $______;
(3)数轴上的两个点之间的距离为$5$,其中一个点表示的数为$2$,则另一个点表示的数为______.

(1)数轴上点$M$,$N表示的数分别为-9和1$,则线段$MN= $______;
(2)数轴上点$E$,$F表示的数分别为-6和-3$,则线段$EF= $______;
(3)数轴上的两个点之间的距离为$5$,其中一个点表示的数为$2$,则另一个点表示的数为______.
答案:
(1)10
(2)3
(3)7或-3
(1)10
(2)3
(3)7或-3
查看更多完整答案,请扫码查看


