第156页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
5. 一个两位数的十位数字与个位数字之和为11. 如果这个两位数加上 45,那么得到的两位数恰好等于原来两位数的十位数字与个位数字交换位置所得到的数,求原来这个两位数.
答案:
解:设原来这个两位数的十位数字为x,则个位数字为11-x.
根据题意,得10x+11-x+45=10(11-x)+x,
解得x=3.
所以10x+11-x=10×3+11-3=38.
答:原来这个两位数是38.
根据题意,得10x+11-x+45=10(11-x)+x,
解得x=3.
所以10x+11-x=10×3+11-3=38.
答:原来这个两位数是38.
6. 在某沙漠地带,汽车每天行驶 200 km,每辆汽车最多可装载行驶 24 天的汽油. 现在甲、乙两辆汽车同时从 A 地出发,规定都必须沿原路返回 A 地. 为了让甲车尽可能开出更远的距离,乙车在行驶一段路程后,仅留足自己返回 A 地的汽油,将其余的汽油补给给甲车,自己返回. 求这样甲车能开出的最远距离.
答案:
解:设乙开出x天后返回,则乙留给甲(24-2x)天的汽油.
根据题意,得(24-x)+(24-2x)=24,
解得x=8.
路程为(24+8)×200×1/2=3200(km).
答:甲车能开出的最远距离是3200 km.
根据题意,得(24-x)+(24-2x)=24,
解得x=8.
路程为(24+8)×200×1/2=3200(km).
答:甲车能开出的最远距离是3200 km.
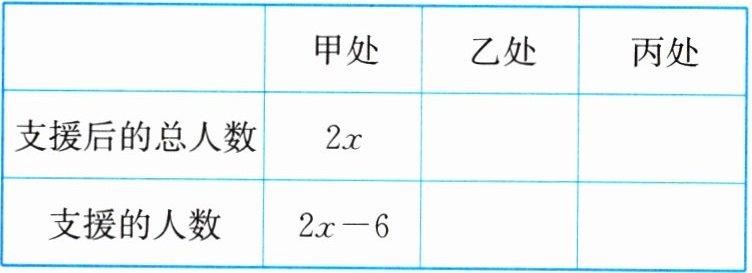
7. 某校组织植树活动,已知在甲处植树的有6人,在乙处植树的有 10 人,在丙处植树的有 8 人,现调来若干人去支援,使在甲、乙、丙三处植树的总人数之比为 2 : 3 : 4. 设支援后在甲处植树的总人数为 2x.
(1)根据信息填表:
| | 甲处 | 乙处 | 丙处 |
| 支援后的总人数 | 2x | | |
| 支援的人数 | 2x - 6 | | |
(2)已知支援丙处的人数是支援乙处的人数的 2 倍,则支援甲、乙、丙三处各有多少人?
(1)根据信息填表:
| | 甲处 | 乙处 | 丙处 |
| 支援后的总人数 | 2x | | |
| 支援的人数 | 2x - 6 | | |

(2)已知支援丙处的人数是支援乙处的人数的 2 倍,则支援甲、乙、丙三处各有多少人?
答案:
解:
(1)填表如下:
| | 甲处 | 乙处 | 丙处 |
| 支援后的总人数 | 2x | 3x | 4x |
| 支援的人数 | 2x - 6 | 3x - 10 | 4x - 8 |
(2)依题意,得4x-8=2(3x-10).
解得x=6.
所以2x-6=6,3x-10=8,4x-8=16.
答:支援甲、乙、丙处各有6人、8人、16人.
(1)填表如下:
| | 甲处 | 乙处 | 丙处 |
| 支援后的总人数 | 2x | 3x | 4x |
| 支援的人数 | 2x - 6 | 3x - 10 | 4x - 8 |
(2)依题意,得4x-8=2(3x-10).
解得x=6.
所以2x-6=6,3x-10=8,4x-8=16.
答:支援甲、乙、丙处各有6人、8人、16人.
8. 某快递公司针对新客户优惠收费,首件物品的收费标准:若质量不超过 10 kg,则免运费;当质量为 x kg(x > 10)时,运费为(2x - 20)元. 第二件物品的收费标准:当质量为 y kg(y > 0)时,运费为(2y + 10)元.
(1)若新客户所寄首件物品的质量为 13 kg,则运费是多少元?
(2)若新客户所寄首件物品的运费为 32 元,则物品的质量是多少千克?
(3)若新客户所寄首件物品与第二件物品的质量之比为 2 : 5,共付运费 50 元,则两件物品的质量各是多少千克?
(1)若新客户所寄首件物品的质量为 13 kg,则运费是多少元?
(2)若新客户所寄首件物品的运费为 32 元,则物品的质量是多少千克?
(3)若新客户所寄首件物品与第二件物品的质量之比为 2 : 5,共付运费 50 元,则两件物品的质量各是多少千克?
答案:
解:
(1)因为13>10,
所以运费为2×13-20=6(元).
答:若新客户所寄首件物品的质量为13 kg,则运费是6元.
(2)由题意,得2x-20=32,解得x=26.
答:若新客户所寄首件物品的运费为32元,则物品的质量是26 kg.
(3)设首件物品的质量为2a kg,则第二件物品的质量为5a kg.
①当0<2a≤10时,2×5a+10=50,解得a=4,
此时2a=8,5a=20;
②当2a>10时,2×2a-20+2×5a+10=50,
解得a=30/7.
因为2×30/7=60/7<10,
所以此情况不符合题意,舍去.
答:首件物品的质量为8 kg,第二件物品的质量为20 kg.
(1)因为13>10,
所以运费为2×13-20=6(元).
答:若新客户所寄首件物品的质量为13 kg,则运费是6元.
(2)由题意,得2x-20=32,解得x=26.
答:若新客户所寄首件物品的运费为32元,则物品的质量是26 kg.
(3)设首件物品的质量为2a kg,则第二件物品的质量为5a kg.
①当0<2a≤10时,2×5a+10=50,解得a=4,
此时2a=8,5a=20;
②当2a>10时,2×2a-20+2×5a+10=50,
解得a=30/7.
因为2×30/7=60/7<10,
所以此情况不符合题意,舍去.
答:首件物品的质量为8 kg,第二件物品的质量为20 kg.
查看更多完整答案,请扫码查看


