第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
1. 整式加减的运算法则
一般地,几个整式相加减,如果有括号就先____,再合并____。
2. 整式的化简求值
整式化简求值的实质是有括号的先去括号,再合并同类项,然后代入求值。
一般地,几个整式相加减,如果有括号就先____,再合并____。
2. 整式的化简求值
整式化简求值的实质是有括号的先去括号,再合并同类项,然后代入求值。
答案:
去括号 同类项
【例1】已知 $ A = a^{2} - 2ab + b^{2} $,$ B = a^{2} + 2ab + b^{2} $。
(1)求 $ A + B $;
(2)求 $ \frac{1}{2}(B - A) $。
(1)求 $ A + B $;
(2)求 $ \frac{1}{2}(B - A) $。
答案:
解:
(1)A+B=(a²-2ab+b²)+(a²+2ab+b²)=a²-2ab+b²+a²+2ab+b²=2a²+2b².
(2) $\frac{1}{2}(B-A)$=$\frac{1}{2}[(a²+2ab+b²)-(a²-2ab+b²)]$=$\frac{1}{2}(a²+2ab+b²-a²+2ab-b²)$=$\frac{1}{2}×4ab$=2ab.
(1)A+B=(a²-2ab+b²)+(a²+2ab+b²)=a²-2ab+b²+a²+2ab+b²=2a²+2b².
(2) $\frac{1}{2}(B-A)$=$\frac{1}{2}[(a²+2ab+b²)-(a²-2ab+b²)]$=$\frac{1}{2}(a²+2ab+b²-a²+2ab-b²)$=$\frac{1}{2}×4ab$=2ab.
(1)几个多项式相减,减式一定要先用括号括起来;
(2)去括号时,要注意符号问题,尤其是有多重括号时;
(3)遇到相同的多项式,可将它视为一个整体进行合并。
(2)去括号时,要注意符号问题,尤其是有多重括号时;
(3)遇到相同的多项式,可将它视为一个整体进行合并。
答案:
(1)几个多项式相减,减式一定要先用括号括起来;
(2)去括号时,要注意符号问题,尤其是有多重括号时;
(3)遇到相同的多项式,可将它视为一个整体进行合并。
(1)几个多项式相减,减式一定要先用括号括起来;
(2)去括号时,要注意符号问题,尤其是有多重括号时;
(3)遇到相同的多项式,可将它视为一个整体进行合并。
1. 计算:
(1)$ -3(2a^{2}b - ab^{2}) - 2(\frac{1}{2}ab^{2} - 2a^{2}b) $;
(2)$ 4xy^{2} - \frac{1}{2}(x^{3}y + 4xy^{2}) - 2[\frac{1}{4}x^{3}y - (x^{2}y - xy^{2})] $。
(1)$ -3(2a^{2}b - ab^{2}) - 2(\frac{1}{2}ab^{2} - 2a^{2}b) $;
(2)$ 4xy^{2} - \frac{1}{2}(x^{3}y + 4xy^{2}) - 2[\frac{1}{4}x^{3}y - (x^{2}y - xy^{2})] $。
答案:
1.解:
(1)-3(2a²b-ab²)-2($\frac{1}{2}ab²-2a²b$)=-6a²b+3ab²-ab²+4a²b=-2a²b+2ab².
(2)4xy²-$\frac{1}{2}(x³y+4xy²)-2[ \frac{1}{4}x³y-(x²y-xy²) ]$=4xy²-$\frac{1}{2}x³y$-2xy²-2($\frac{1}{4}x³y-x²y+xy²$)=4xy²-$\frac{1}{2}x³y$-2xy²-$\frac{1}{2}x³y$+2x²y-2xy²=-x³y+2x²y.
(1)-3(2a²b-ab²)-2($\frac{1}{2}ab²-2a²b$)=-6a²b+3ab²-ab²+4a²b=-2a²b+2ab².
(2)4xy²-$\frac{1}{2}(x³y+4xy²)-2[ \frac{1}{4}x³y-(x²y-xy²) ]$=4xy²-$\frac{1}{2}x³y$-2xy²-2($\frac{1}{4}x³y-x²y+xy²$)=4xy²-$\frac{1}{2}x³y$-2xy²-$\frac{1}{2}x³y$+2x²y-2xy²=-x³y+2x²y.
【例2】(教材例题变式)现要做大、小长方体纸盒各一个,尺寸如下(单位:cm):
|纸盒|长|宽|高|
|小纸盒| $ 2a $ | $ 3b $ | $ c $ |
|大纸盒| $ 3a $ | $ 4b $ | $ 2c $ |
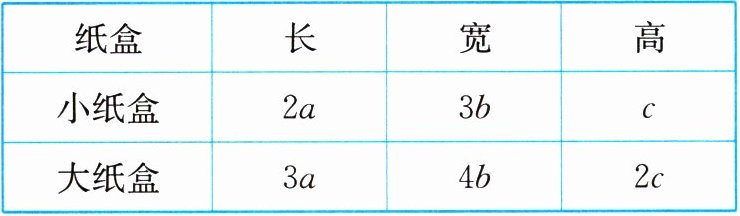
(1)做大纸盒比做小纸盒多用多少平方厘米材料?
(2)当 $ a = 10 $,$ b = 5 $,$ c = 2 $ 时,做这两个纸盒共用多少平方厘米材料?
|纸盒|长|宽|高|
|小纸盒| $ 2a $ | $ 3b $ | $ c $ |
|大纸盒| $ 3a $ | $ 4b $ | $ 2c $ |

(1)做大纸盒比做小纸盒多用多少平方厘米材料?
(2)当 $ a = 10 $,$ b = 5 $,$ c = 2 $ 时,做这两个纸盒共用多少平方厘米材料?
答案:
解:
(1)2(2a·3b+2ac+3bc)=12ab+4ac+6bc(cm²),2(3a·4b+3a·2c+4b·2c)=24ab+12ac+16bc(cm²).做一个大纸盒比做一个小纸盒多用(24ab+12ac+16bc)-(12ab+4ac+6bc)=(12ab+8ac+10bc)(cm²)材料.
(2)当a=10,b=5,c=2时,材料共用12ab+4ac+6bc+24ab+12ac+16bc=36ab+16ac+22bc=36×10×5+16×10×2+22×5×2=2340(cm²).
(1)2(2a·3b+2ac+3bc)=12ab+4ac+6bc(cm²),2(3a·4b+3a·2c+4b·2c)=24ab+12ac+16bc(cm²).做一个大纸盒比做一个小纸盒多用(24ab+12ac+16bc)-(12ab+4ac+6bc)=(12ab+8ac+10bc)(cm²)材料.
(2)当a=10,b=5,c=2时,材料共用12ab+4ac+6bc+24ab+12ac+16bc=36ab+16ac+22bc=36×10×5+16×10×2+22×5×2=2340(cm²).
查看更多完整答案,请扫码查看


