第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1 圈一圈,填一填。
篮球小组有 35 人,每队 5 人,可以分成几队?
□○□=□( )
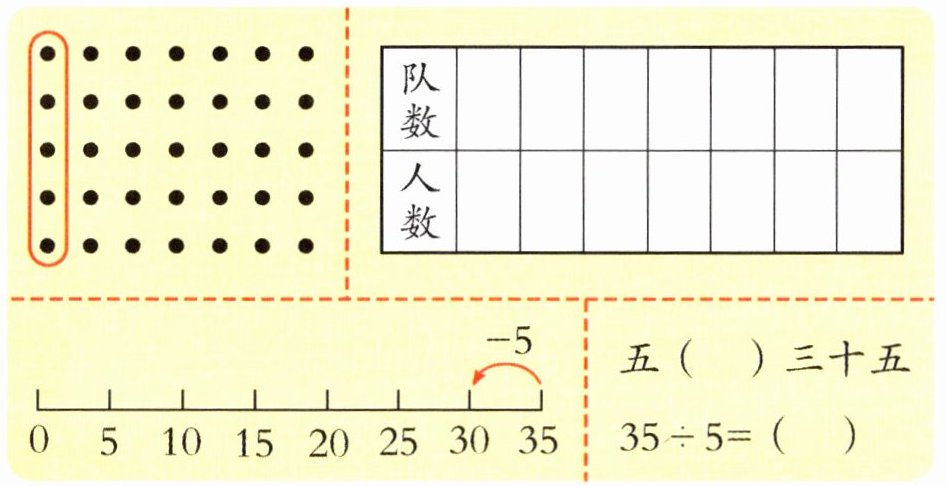
答:可以分成___队。
篮球小组有 35 人,每队 5 人,可以分成几队?
□○□=□( )

答:可以分成___队。
答案:
解析:本题考查除法的意义以及乘法口诀的运用。通过圈一圈的方式,将$35$人按每$5$人一组进行分组,实际就是求$35$里面有几个$5$,用除法计算,同时借助乘法口诀来得出结果。
答案:$35÷5 = 7$(队)
答:可以分成$7$队。
答案:$35÷5 = 7$(队)
答:可以分成$7$队。
2 24个几次能运完?______

答:___次能运完。
6个我已经运了3次。
还剩下几个苹果?______
答:还剩下___个苹果。

答:___次能运完。
6个我已经运了3次。
还剩下几个苹果?______
答:还剩下___个苹果。
答案:
解析:
题目考查有余数的除法应用。
第一问,已知有$24$个苹果,小刺猬每次运$6$个,求运完的次数,就是求$24$里有几个$6$,用除法计算,$24÷6 = 4$(次)。
第二问,已知小刺猬已经运了$3$次,每次运$6$个,那么运走的苹果数为$3×6 = 18$(个),用苹果总数$24$减去运走的$18$个,可得剩下的苹果数为$24 - 18 = 6$(个)。
答案:
$4$;$4$;$6$;$6$;
题目考查有余数的除法应用。
第一问,已知有$24$个苹果,小刺猬每次运$6$个,求运完的次数,就是求$24$里有几个$6$,用除法计算,$24÷6 = 4$(次)。
第二问,已知小刺猬已经运了$3$次,每次运$6$个,那么运走的苹果数为$3×6 = 18$(个),用苹果总数$24$减去运走的$18$个,可得剩下的苹果数为$24 - 18 = 6$(个)。
答案:
$4$;$4$;$6$;$6$;
笑笑按规律摆出下面这组图形,共用去 54 个图形,
(1) 有( )个。□○□= □( )
有( )个。□○□= □( )
(2) 有( )个。□○□= □( )
有( )个。□○□= □( )
(3) 有( )个。□○□= □( )
有( )个。□○□= □( )

(1)
 有( )个。□○□= □( )
有( )个。□○□= □( )(2)
 有( )个。□○□= □( )
有( )个。□○□= □( )(3)
 有( )个。□○□= □( )
有( )个。□○□= □( )
答案:
解析:本题可先找出图形的排列规律,计算出循环周期的数量,再根据每种图形在每个周期中的数量,计算出每种图形的总数。
步骤一:分析图形排列规律
观察这组图形“$○\triangle\triangle□□□○\triangle\triangle□□□\cdots\cdots$”,可以发现它是以“$○\triangle\triangle□□□$”这$6$个图形为一组循环出现的,即循环周期为$6$。
步骤二:计算循环周期的数量
已知共用去$54$个图形,用图形总数除以每个周期的图形数,可得循环周期的数量为:$54÷6 = 9$(组)
步骤三:分别计算每种图形的数量
计算$○$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$○$有$1$个,一共有$9$个周期,所以$○$的总数为:$1×9 = 9$(个)
算式为:$54÷6×1 = 9$(个)
计算$\triangle$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$\triangle$有$2$个,一共有$9$个周期,所以$\triangle$的总数为:$2×9 = 18$(个)
算式为:$54÷6×2 = 18$(个)
计算$□$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$□$有$3$个,一共有$9$个周期,所以$□$的总数为:$3×9 = 27$(个)
算式为:$54÷6×3 = 27$(个)
答案:
(1)$9$;$54÷6×1 = 9$(个)
(2)$18$;$54÷6×2 = 18$(个)
(3)$27$;$54÷6×3 = 27$(个)
步骤一:分析图形排列规律
观察这组图形“$○\triangle\triangle□□□○\triangle\triangle□□□\cdots\cdots$”,可以发现它是以“$○\triangle\triangle□□□$”这$6$个图形为一组循环出现的,即循环周期为$6$。
步骤二:计算循环周期的数量
已知共用去$54$个图形,用图形总数除以每个周期的图形数,可得循环周期的数量为:$54÷6 = 9$(组)
步骤三:分别计算每种图形的数量
计算$○$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$○$有$1$个,一共有$9$个周期,所以$○$的总数为:$1×9 = 9$(个)
算式为:$54÷6×1 = 9$(个)
计算$\triangle$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$\triangle$有$2$个,一共有$9$个周期,所以$\triangle$的总数为:$2×9 = 18$(个)
算式为:$54÷6×2 = 18$(个)
计算$□$的数量:
在每个周期“$○\triangle\triangle□□□$”中,$□$有$3$个,一共有$9$个周期,所以$□$的总数为:$3×9 = 27$(个)
算式为:$54÷6×3 = 27$(个)
答案:
(1)$9$;$54÷6×1 = 9$(个)
(2)$18$;$54÷6×2 = 18$(个)
(3)$27$;$54÷6×3 = 27$(个)
查看更多完整答案,请扫码查看


