第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
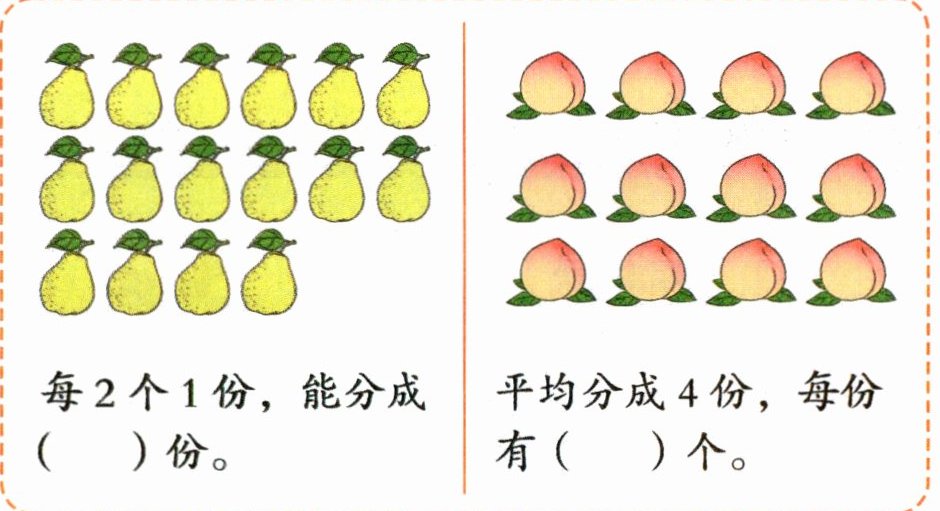
1 圈一圈,填一填。

答案:
解析:本题考查除法的初步认识,即包含除和平均分的知识点。对于第一组图形,通过圈一圈的方式,将梨每$2$个分为一份,数出份数;对于第二组图形,将桃子平均分成$4$份,数出每份的个数。
答案:
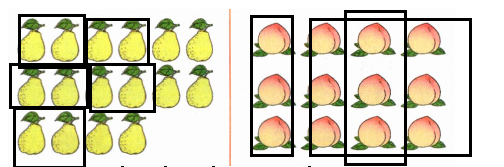
每$2$个$1$份,能分成( $6$ )份。
平均分成$4$份,每份有( $3$ )个。
解析:本题考查除法的初步认识,即包含除和平均分的知识点。对于第一组图形,通过圈一圈的方式,将梨每$2$个分为一份,数出份数;对于第二组图形,将桃子平均分成$4$份,数出每份的个数。
答案:

每$2$个$1$份,能分成( $6$ )份。
平均分成$4$份,每份有( $3$ )个。
2
一共有( )个橘子,每5个装一袋,可以装( )袋。
算式:□○□= □( )
读作:( )。

一共有( )个橘子,每5个装一袋,可以装( )袋。
算式:□○□= □( )
读作:( )。
答案:
本题可先数出橘子的总数,再根据除法的意义计算装的袋数,最后写出算式的读法。
步骤一:数出橘子的总数
通过观察图片可知,一共有$10$个橘子。
步骤二:计算装的袋数
已知每$5$个装一袋,求可以装几袋,就是求$10$里面有几个$5$,用除法计算,算式为$10÷5 = 2$(袋)。
步骤三:写出算式的读法
$10÷5 = 2$读作:$10$除以$5$等于$2$。
综上,答案依次为:$\boldsymbol{10}$;$\boldsymbol{2}$;$\boldsymbol{10÷5 = 2}$(袋);$\boldsymbol{10}$除以$\boldsymbol{5}$等于$\boldsymbol{2}$。
步骤一:数出橘子的总数
通过观察图片可知,一共有$10$个橘子。
步骤二:计算装的袋数
已知每$5$个装一袋,求可以装几袋,就是求$10$里面有几个$5$,用除法计算,算式为$10÷5 = 2$(袋)。
步骤三:写出算式的读法
$10÷5 = 2$读作:$10$除以$5$等于$2$。
综上,答案依次为:$\boldsymbol{10}$;$\boldsymbol{2}$;$\boldsymbol{10÷5 = 2}$(袋);$\boldsymbol{10}$除以$\boldsymbol{5}$等于$\boldsymbol{2}$。
3 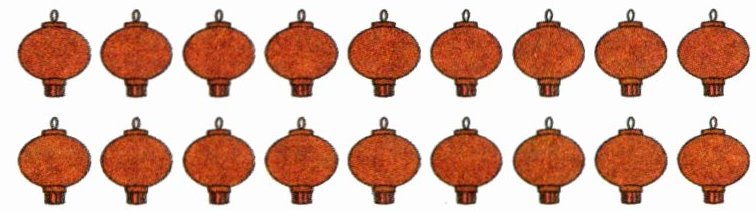
(1)一共有( )个灯笼。
(2)每3个穿一串,可以穿( )串。
(3)每6个穿一串,可以穿( )串。

(1)一共有( )个灯笼。
(2)每3个穿一串,可以穿( )串。
(3)每6个穿一串,可以穿( )串。
答案:
(1)18
(2)6
(3)3
(1)18
(2)6
(3)3
查看更多完整答案,请扫码查看


