《2025年课堂练习二年级数学上册北师大版》

1 下列分法是平均分的是( )。(填序号)

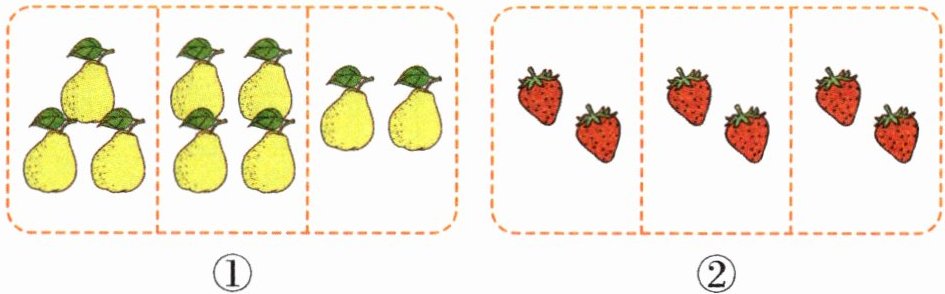
答案： ②

2 把 12 根胡萝卜平均分给 4 只小兔,你会怎样分？画一画。(用|代表胡萝卜)

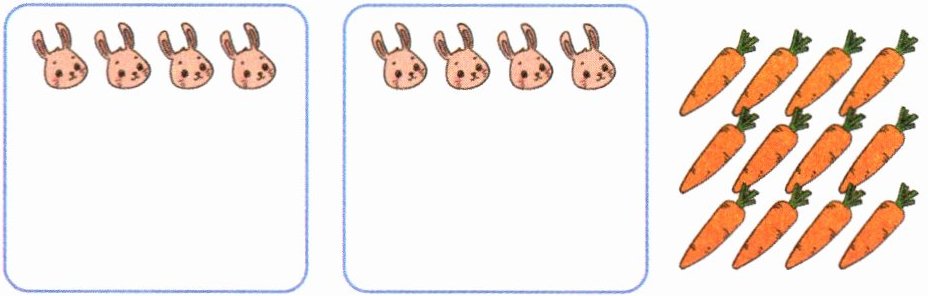
每只小兔可以分到( )根胡萝卜。

答案： | | |
| | |
| | |
| | |
3

圈一圈,填一填。
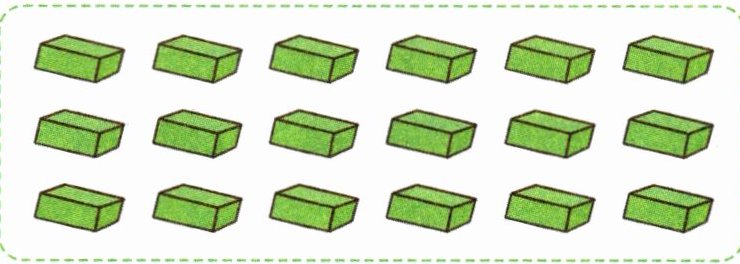
有 18 块积木,把它们平均分成若干份(不能一次分完),有( )种不同分法。

答案： 解析：本题可根据因数的概念，找出$18$的所有因数（$1$和$18$除外），进而确定平均分的不同分法。
因数是指整数$a$除以整数$b(b\neq0)$ 的商正好是整数而没有余数，此时称$b$是$a$的因数。
因为$18 = 1×18 = 2×9 = 3×6$，所以$18$的因数有$1$、$2$、$3$、$6$、$9$、$18$。
题目要求平均分成若干份且不能一次分完，即份数不能为$1$，同时也不能把$18$块积木全部分成$1$块一份，也就是份数不能为$18$。
那么符合条件的因数有$2$、$3$、$6$、$9$这$4$个。
当份数为$2$时，每份有$18÷2 = 9$块；当份数为$3$时，每份有$18÷3 = 6$块；当份数为$6$时，每份有$18÷6 = 3$块；当份数为$9$时，每份有$18÷9 = 2$块。
所以有$4$种不同分法。
答案：4