1.下列各式计算正确的是 ( )
A.6+a= 6a
B.6a+a= 6a
C.6a-a= 6
D.6a-a= 5a
A.6+a= 6a
B.6a+a= 6a
C.6a-a= 6
D.6a-a= 5a
答案:
D
2.如果一个长方形的周长是6m,其中长方形的长是2m+2n,那么宽为 ( )
A.m+n
B.4m-2n
C.m-2n
D.4m+2n
A.m+n
B.4m-2n
C.m-2n
D.4m+2n
答案:
C
3.设$M= x^2+3x+7,N= -x^2+3x-4,$那么M与N的大小关系是 ( )
A.M<N
B.M= N
C.M>N
D.无法确定
A.M<N
B.M= N
C.M>N
D.无法确定
答案:
C
4.计算$6a^2-5a+3$与$5a^2+2a-1$的差,结果正确的是 ( )
$A.a^2-3a+4 B.a^2-3a+2$
$C.a^2-7a+2 D.a^2-7a+4$
$A.a^2-3a+4 B.a^2-3a+2$
$C.a^2-7a+2 D.a^2-7a+4$
答案:
D
5.【淮安】去括号并合并同类项:3a-(2a-b)= 。
答案:
a+b
6.有三个连续的偶数,设最小的一个为2n,那么它们的和可表示为 。
答案:
6n+6
7.已知$A= 4x^2-4xy+y^2,B= x^2+xy-5y^2,$计算:A-3B= 。
答案:
x²-7xy+16y²
8.化简:
(1)2(2a-b)-(2b-3a)。
$(2)2(xy^2-x^2y)-3(x^2y+xy^2-1)。$
(1)2(2a-b)-(2b-3a)。
$(2)2(xy^2-x^2y)-3(x^2y+xy^2-1)。$
答案:
(1)原式=4a-2b-2b+3a=7a-4b。
(2)原式=2xy²-2x²y-3x²y-3xy²+3=-5x²y-xy²+3。
(1)原式=4a-2b-2b+3a=7a-4b。
(2)原式=2xy²-2x²y-3x²y-3xy²+3=-5x²y-xy²+3。
9.先化简,再求值:
$(1)3(x^2-2)-2(x^2-2x-3),$其中x= -2。
$(2)xy-(3x^2+5xy-y^2)+3(x^2+2xy),$其中x= 2,y= -1。
$(1)3(x^2-2)-2(x^2-2x-3),$其中x= -2。
$(2)xy-(3x^2+5xy-y^2)+3(x^2+2xy),$其中x= 2,y= -1。
答案:
(1)原式=3x²-6-2x²+4x+6=x²+4x。当x=-2时,原式=(-2)²+4×(-2)=-4。
(2)原式=xy-3x²-5xy+y²+3x²+6xy=2xy+y²,当x=2,y=-1时,原式=2×2×(-1)+(-1)²=-3。
(1)原式=3x²-6-2x²+4x+6=x²+4x。当x=-2时,原式=(-2)²+4×(-2)=-4。
(2)原式=xy-3x²-5xy+y²+3x²+6xy=2xy+y²,当x=2,y=-1时,原式=2×2×(-1)+(-1)²=-3。
10.对于有理数a,b,定义a⊙b= 3a+2b,则(x+y)⊙(x-y)化简后得 ( )
A.5x+y
B.5x
C.2x
D.5x-y
A.5x+y
B.5x
C.2x
D.5x-y
答案:
A
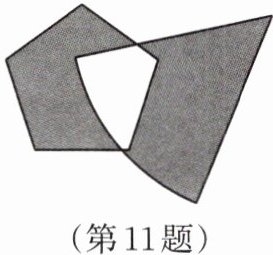
11.如图所示,正五边形的面积为$2m^2-3m,$扇形的面积为9+5m,空白部分的面积为$m^2,$则图中两块阴影部分的面积和为 ( )
$A.m^2+2m+9 B.2m+9$
$C.m^2-8m-9 D.8m+9$
]
$A.m^2+2m+9 B.2m+9$
$C.m^2-8m-9 D.8m+9$
]

答案:
B
查看更多完整答案,请扫码查看


