12.如图所示,在数轴上标注了三段范围,则表示$\sqrt{8}$的点落在第 段内。


答案:
③
13.如图所示,每个小正方形的边长均为1,观察图形,回答问题。
(1)图中阴影部分的面积和边长是多少?
(2)估计边长的值在哪两个整数之间。
(3)把边长在数轴上表示出来。
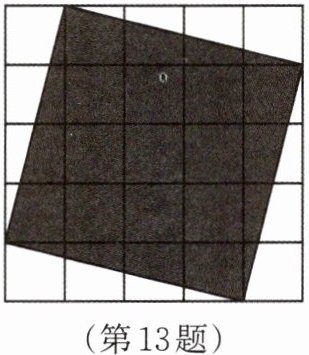
(1)图中阴影部分的面积和边长是多少?
(2)估计边长的值在哪两个整数之间。
(3)把边长在数轴上表示出来。

答案:
(1)图中阴影部分的面积$S=17$,边长是$\sqrt{17}$。
(2)因为$4^2=16$,$5^2=25$,所以边长的值在4与5之间。
(3)略
(1)图中阴影部分的面积$S=17$,边长是$\sqrt{17}$。
(2)因为$4^2=16$,$5^2=25$,所以边长的值在4与5之间。
(3)略
14.如图所示为一个数值转换器。

(1)当输入的x值为16时,求输出的y值。
(2)是否存在输入x值后,始终输不出y值的情况?如果存在,请直接写出所有满足要求的x值;如果不存在,请说明理由。
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则x= 。

(1)当输入的x值为16时,求输出的y值。
(2)是否存在输入x值后,始终输不出y值的情况?如果存在,请直接写出所有满足要求的x值;如果不存在,请说明理由。
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则x= 。
答案:
(1)因为$\sqrt{16}=4$,$\sqrt{4}=2$,所以$y=\sqrt{2}$。
(2)存在。当$x=0$或1时,始终输不出y值。
(3)25或36或49或64
(1)因为$\sqrt{16}=4$,$\sqrt{4}=2$,所以$y=\sqrt{2}$。
(2)存在。当$x=0$或1时,始终输不出y值。
(3)25或36或49或64
15.阅读下列信息材料:
信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部写出来,比如:π,$\sqrt{2}$等,而常用的"…"或者"≈"的表示方法都不够百分百准确;
信息2:2.5的整数部分是2,小数部分是0.5,可以看成2.5-2得来的;
信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如:$2<\sqrt{5}<3$,是因为$\sqrt{4}<\sqrt{5}<\sqrt{9}$。
根据上述信息,回答下列问题:
(1)$\sqrt{13}$的整数部分是 ,小数部分是 。
(2)若21<a<22,则a的整数部分是 ;小数部分可以表示为 。
(3)$10+\sqrt{3}$也是夹在两个相邻整数之间的,可以表示为$a<10+\sqrt{3}<b$,则a+b= 。
(4)若$\sqrt{30}-3= x+y$,其中x是整数,且0<y<1,请求出x-y的相反数。
信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部写出来,比如:π,$\sqrt{2}$等,而常用的"…"或者"≈"的表示方法都不够百分百准确;
信息2:2.5的整数部分是2,小数部分是0.5,可以看成2.5-2得来的;
信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如:$2<\sqrt{5}<3$,是因为$\sqrt{4}<\sqrt{5}<\sqrt{9}$。
根据上述信息,回答下列问题:
(1)$\sqrt{13}$的整数部分是 ,小数部分是 。
(2)若21<a<22,则a的整数部分是 ;小数部分可以表示为 。
(3)$10+\sqrt{3}$也是夹在两个相邻整数之间的,可以表示为$a<10+\sqrt{3}<b$,则a+b= 。
(4)若$\sqrt{30}-3= x+y$,其中x是整数,且0<y<1,请求出x-y的相反数。
答案:
(1)因为$\sqrt{9}<\sqrt{13}<\sqrt{16}$,所以$3<\sqrt{13}<4$。
所以$\sqrt{13}$的整数部分是3,小数部分是$\sqrt{13}-3$。
故答案为:$3$;$\sqrt{13}-3$。
(2)21 $a-21$
(3)因为$\sqrt{1}<\sqrt{3}<\sqrt{4}$,所以$1<\sqrt{3}<2$。
所以$11<10+\sqrt{3}<12$。
所以$a=11$,$b=12$。所以$a+b=11+12=23$。
故答案为:23。
(4)因为$\sqrt{25}<\sqrt{30}<\sqrt{36}$,所以$5<\sqrt{30}<6$。
所以$2<\sqrt{30}-3<3$。又因为x是整数,且$0<y<1$,
所以$x=2$,$y=(\sqrt{30}-3)-2=\sqrt{30}-5$。
所以$x-y=2-(\sqrt{30}-5)=7-\sqrt{30}$。
所以$x-y$的相反数是$\sqrt{30}-7$。
(1)因为$\sqrt{9}<\sqrt{13}<\sqrt{16}$,所以$3<\sqrt{13}<4$。
所以$\sqrt{13}$的整数部分是3,小数部分是$\sqrt{13}-3$。
故答案为:$3$;$\sqrt{13}-3$。
(2)21 $a-21$
(3)因为$\sqrt{1}<\sqrt{3}<\sqrt{4}$,所以$1<\sqrt{3}<2$。
所以$11<10+\sqrt{3}<12$。
所以$a=11$,$b=12$。所以$a+b=11+12=23$。
故答案为:23。
(4)因为$\sqrt{25}<\sqrt{30}<\sqrt{36}$,所以$5<\sqrt{30}<6$。
所以$2<\sqrt{30}-3<3$。又因为x是整数,且$0<y<1$,
所以$x=2$,$y=(\sqrt{30}-3)-2=\sqrt{30}-5$。
所以$x-y=2-(\sqrt{30}-5)=7-\sqrt{30}$。
所以$x-y$的相反数是$\sqrt{30}-7$。
查看更多完整答案,请扫码查看


