《2025年经纶学典课时作业七年级数学上册苏科版》

19. 如图所示,小明有标注①~⑤号的5张写着不同有理数的卡片,请你按要求选出卡片,完成下列各题.

(1)从中选出1张卡片,且这张卡片的有理数在全部有理数大小排列里居中,应选取②号卡片；
(2)从中选出2张卡片,且这2张卡片的有理数差最大,应选取④⑤号卡片,差的最大值是14；
(3)从中选出3张卡片,且这3张卡片的有理数积最小,应选取①④⑤号卡片,积的最小值是-144；
(4)从中选出4张卡片,且将这4张卡片的有理数运用加、减、乘和除四则运算及括号列出一个算式,使得该算式的计算结果为24,请你写出算式(只需写出1种即可).
$[-1 - (6 ÷ 3)] × (-8) = 24$

答案：
(1)② 解析：因为$-8 ＜ -4 ＜ -1 ＜ 3 ＜ 6$，所以在5个有理数的大小排列里居中的数是-1，所以选②号卡片.
(2)④⑤ 14 解析：当选取卡片④⑤时，差值最大，差的最大值是$6 - (-8) = 14$.
(3)①④⑤ -144 解析：当选取卡片①④⑤时，乘积最小，积的最小值是$(-8) × 6 × 3 = -144$.
(4)答案不唯一，如选取①②④⑤四张卡片.$[-1 - (6 ÷ 3)] × (-8) = (-1 - 2) × (-8) = (-3) × (-8) = 24$

20. A,B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如表.

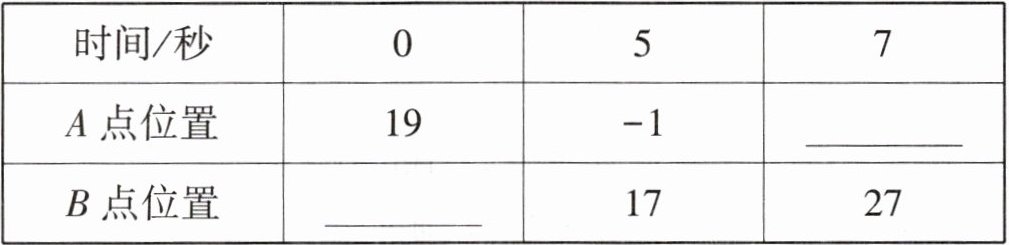
(1)填写表格中的横线.
(2)A,B两点能否相遇？如果相遇,求相遇时的时刻及在数轴上的位置；如果不能相遇,请说明理由.
(3)A,B两点能否相距9个单位长度？如果能,求相距9个单位长度的时刻；如果不能,请说明理由.
(1)填表如下：时间/秒057A点位置19-1-9B点位置-81727
(2)能相遇，根据题意可得[19 - (-8)] ÷ (4 + 5) = 3（秒），19 - 3 × 4 = 7，所以在第3秒时相遇，此时在数轴上7的位置.
(3)A,B两点能相距9个单位长度.第一种：A,B相遇前相距9个单位长度，[19 - (-8) - 9] ÷ (4 + 5) = 2（秒）.第二种：A,B相遇后相距9个单位长度，[19 - (-8) + 9] ÷ (4 + 5) = 4（秒），所以能在第2秒或第4秒时相距9个单位长度.

答案：
(1)填表如下：时间/秒057A点位置19-1-9B点位置-81727
(2)能相遇，根据题意可得$[19 - (-8)] ÷ (4 + 5) = 3$（秒），$19 - 3 × 4 = 7$，所以在第3秒时相遇，此时在数轴上7的位置.
(3)A,B两点能相距9个单位长度.第一种：A,B相遇前相距9个单位长度，$[19 - (-8) - 9] ÷ (4 + 5) = 2$（秒）.第二种：A,B相遇后相距9个单位长度，$[19 - (-8) + 9] ÷ (4 + 5) = 4$（秒），所以能在第2秒或第4秒时相距9个单位长度.