7. 将下图中的6个角按从大到小的顺序排列:(
①>⑥>⑤>③>②>④
)。
答案:
①>⑥>⑤>③>②>④
8. 下午5时整,钟面上时针与分针所成的较小角为(
150
)度。一个小时后,钟面上时针与分针成(平
)角,这段时间分针走了(360
)度。
答案:
下午5时整,钟面共12个大格,每个大格为360÷12=30度,时针指向5,分针指向12,中间有5个大格,较小角为5×30=150度。
一个小时后是下午6时整,时针指向6,分针指向12,中间有6个大格,夹角为6×30=180度,是平角。
这段时间分针从12走到12,走了一圈,即360度。
150;平;360
一个小时后是下午6时整,时针指向6,分针指向12,中间有6个大格,夹角为6×30=180度,是平角。
这段时间分针从12走到12,走了一圈,即360度。
150;平;360
1. (
A.10
B.15
C.25
B
)度的角能用一副三角板画出来。A.10
B.15
C.25
答案:
解析:本题考查的是对三角板中各个角的度数的了解以及利用这些角度通过加、减等方法组合出新的角度。我们知道一副常规的三角板中有两种三角形,其角度分别为$30^\circ$、$60^\circ$、$90^\circ$和$45^\circ$、$45^\circ$、$90^\circ$。通过这些角度的组合,我们可以得到如$30^\circ+45^\circ=75^\circ$,$45^\circ-30^\circ=15^\circ$等角度。
接下来,我们逐一分析选项:
A选项:$10^\circ$的角无法通过三角板中的角度组合得到。
B选项:$15^\circ$的角可以通过$45^\circ-30^\circ$得到,或者通过$60^\circ-45^\circ$得到,因此是可以用三角板画出来的。
C选项:$25^\circ$的角同样无法通过三角板中的角度组合得到。
答案:B.15。
接下来,我们逐一分析选项:
A选项:$10^\circ$的角无法通过三角板中的角度组合得到。
B选项:$15^\circ$的角可以通过$45^\circ-30^\circ$得到,或者通过$60^\circ-45^\circ$得到,因此是可以用三角板画出来的。
C选项:$25^\circ$的角同样无法通过三角板中的角度组合得到。
答案:B.15。
2. 任意一个三角形中至少有(
A.3
B.2
C.1
B
)个锐角。A.3
B.2
C.1
答案:
解析:本题可根据三角形的内角和以及角的分类来分析三角形中锐角的个数。
三角形的内角和是$180^{\circ}$,角分为锐角(小于$90^{\circ}$)、直角(等于$90^{\circ}$)、钝角(大于$90^{\circ}$小于$180^{\circ}$)。
假设一个三角形中只有$1$个锐角,那么另外两个角可能是直角或钝角。
如果另外两个角都是直角,那么三个角的和为$90^{\circ}+90^{\circ}+锐角\gt180^{\circ}$,不满足三角形内角和是$180^{\circ}$。
如果另外两个角都是钝角,那么三个角的和也会大于$180^{\circ}$,同样不满足三角形内角和是$180^{\circ}$。
所以一个三角形中不可能只有$1$个锐角。
假设一个三角形中没有锐角,即三个角都是直角或钝角,那么三个角的和必然大于$180^{\circ}$,也不满足三角形内角和是$180^{\circ}$。
而当三角形中有$2$个锐角时,比如两个锐角分别为$30^{\circ}$和$60^{\circ}$,那么第三个角可以是$180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$,是合理的。
当三角形中有$3$个锐角时,比如三个角都是$60^{\circ}$,也满足三角形内角和是$180^{\circ}$。
所以任意一个三角形中至少有$2$个锐角。
答案:B。
三角形的内角和是$180^{\circ}$,角分为锐角(小于$90^{\circ}$)、直角(等于$90^{\circ}$)、钝角(大于$90^{\circ}$小于$180^{\circ}$)。
假设一个三角形中只有$1$个锐角,那么另外两个角可能是直角或钝角。
如果另外两个角都是直角,那么三个角的和为$90^{\circ}+90^{\circ}+锐角\gt180^{\circ}$,不满足三角形内角和是$180^{\circ}$。
如果另外两个角都是钝角,那么三个角的和也会大于$180^{\circ}$,同样不满足三角形内角和是$180^{\circ}$。
所以一个三角形中不可能只有$1$个锐角。
假设一个三角形中没有锐角,即三个角都是直角或钝角,那么三个角的和必然大于$180^{\circ}$,也不满足三角形内角和是$180^{\circ}$。
而当三角形中有$2$个锐角时,比如两个锐角分别为$30^{\circ}$和$60^{\circ}$,那么第三个角可以是$180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$,是合理的。
当三角形中有$3$个锐角时,比如三个角都是$60^{\circ}$,也满足三角形内角和是$180^{\circ}$。
所以任意一个三角形中至少有$2$个锐角。
答案:B。
3. 右边正方形中能数出(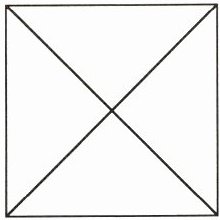
A.4
B.6
C.8
C
)个直角。
A.4
B.6
C.8
答案:
解析:本题考查对直角概念的理解以及数图形中直角个数的知识点。正方形本身有$4$个直角,两条对角线相交会形成$4$个直角,所以总共能数出的直角个数为$4 + 4 = 8$个。
答案:C。
答案:C。
4. 平平和聪聪描同一块三角板(如图)中的最小角,平平描出的角是①,聪聪描出的角是②,那么①和②的大小关系是(
A.①>②
B.①<②
C.①=②
D.无法比较
C
)。
A.①>②
B.①<②
C.①=②
D.无法比较
答案:
解析:根据角的定义,角是由一个顶点和两条边组成的图形,角的大小只与角的两边张开的程度有关,与边的长短无关。
平平描出的角①和聪聪描出的角②,它们都是三角板上的同一个最小角,只是描出的边的长短不同,但角的两边张开的程度是一样的,所以这两个角的大小相等。
答案:C。
平平描出的角①和聪聪描出的角②,它们都是三角板上的同一个最小角,只是描出的边的长短不同,但角的两边张开的程度是一样的,所以这两个角的大小相等。
答案:C。
查看更多完整答案,请扫码查看


