1. 已知48÷3=16,那么4800÷(
已知960÷40=24,那么(
300
)=16。已知960÷40=24,那么(
480
)÷20=24。
答案:
解析:
第一个问题考查的是除法的商不变规律。当被除数扩大(或缩小)若干倍,除数也扩大(或缩小)相同的倍数时,商是不变的。已知48÷3=16,现在被除数变成了4800,是原来的100倍,所以除数也应该是原来的100倍,即3×100=300,才能保持商为16。
第二个问题同样考查商不变的规律。已知960÷40=24,现在除数变成了20,是原来的一半,所以被除数也应该是原来的一半,即960÷2=480,才能保持商为24。
答案:
1. 已知48÷3=16,那么4800÷
(300)=16。
2. 已知960÷40=24,那么
(480)÷20=24。
第一个问题考查的是除法的商不变规律。当被除数扩大(或缩小)若干倍,除数也扩大(或缩小)相同的倍数时,商是不变的。已知48÷3=16,现在被除数变成了4800,是原来的100倍,所以除数也应该是原来的100倍,即3×100=300,才能保持商为16。
第二个问题同样考查商不变的规律。已知960÷40=24,现在除数变成了20,是原来的一半,所以被除数也应该是原来的一半,即960÷2=480,才能保持商为24。
答案:
1. 已知48÷3=16,那么4800÷
(300)=16。
2. 已知960÷40=24,那么
(480)÷20=24。
2. 在算式□÷31=3……△中,□中的数最大是(
123
),最小是(94
)。
答案:
解析:
本题考查有余数的除法。
在有余数的除法中,余数总比除数小,即余数最大为:除数-1,最小为1。
当余数最大时,被除数最大,当余数最小时,被除数最小。
根据“被除数=商×除数+余数”解答即可。
余数最大为:31-1=30
被除数最大为:3×31+30=123
余数最小为1
被除数最小为:3×31+1=94
答案:
□中的数最大是
(123),最小是
(94)。
本题考查有余数的除法。
在有余数的除法中,余数总比除数小,即余数最大为:除数-1,最小为1。
当余数最大时,被除数最大,当余数最小时,被除数最小。
根据“被除数=商×除数+余数”解答即可。
余数最大为:31-1=30
被除数最大为:3×31+30=123
余数最小为1
被除数最小为:3×31+1=94
答案:
□中的数最大是
(123),最小是
(94)。
3. 要使374÷27的余数为0,被除数至少减去(
23
)。
答案:
解析:
首先,我们要理解题目的意思:找到一个数,使得374减去这个数后能被27整除。
为了找到这个数,我们可以先找到374除以27的商和余数。
$374 ÷ 27 = 13\ldots\ldots 23$,余数是23。
这意味着,如果我们从374中减去23,那么结果就可以被27整除。
所以,为了使374除以27的余数为0,被除数至少需要减去23。
答案:
23
首先,我们要理解题目的意思:找到一个数,使得374减去这个数后能被27整除。
为了找到这个数,我们可以先找到374除以27的商和余数。
$374 ÷ 27 = 13\ldots\ldots 23$,余数是23。
这意味着,如果我们从374中减去23,那么结果就可以被27整除。
所以,为了使374除以27的余数为0,被除数至少需要减去23。
答案:
23
4. 下面的( )里,最大填几?
40×(
40×(
5
)<210 52×(6
)<319 25×(8
)<210
答案:
解析:
本题考查的是利用除法来解决实际问题。
需要找到一个数字填入括号,使得这个乘积小于给定的数,并且要求这个数字是最大的。
对于第一个问题:40×( )<210,
可以用210除以40,得到的结果取整数部分,即最大的填数。
210 ÷ 40 = 5......10,
所以,最大的填数是5,因为40×5=200,小于210。
对于第二个问题:52×( )<319,
可以用319除以52,得到的结果取整数部分。
319 ÷ 52 = 6......7,
所以,最大的填数是6,因为52×6=312,小于319。
对于第三个问题:25×( )<210,
可以用210除以25,得到的结果取整数部分。
210 ÷ 25 = 8......10,
所以,最大的填数是8,因为25×8=200,小于210。
答案:
40×
(5)<210,
52×
(6)<319,
25×
(8)<210。
本题考查的是利用除法来解决实际问题。
需要找到一个数字填入括号,使得这个乘积小于给定的数,并且要求这个数字是最大的。
对于第一个问题:40×( )<210,
可以用210除以40,得到的结果取整数部分,即最大的填数。
210 ÷ 40 = 5......10,
所以,最大的填数是5,因为40×5=200,小于210。
对于第二个问题:52×( )<319,
可以用319除以52,得到的结果取整数部分。
319 ÷ 52 = 6......7,
所以,最大的填数是6,因为52×6=312,小于319。
对于第三个问题:25×( )<210,
可以用210除以25,得到的结果取整数部分。
210 ÷ 25 = 8......10,
所以,最大的填数是8,因为25×8=200,小于210。
答案:
40×
(5)<210,
52×
(6)<319,
25×
(8)<210。
5. □51÷45,要使商是两位数,□里可以填
4,5,6,7,8,9
;若商是一位数,□里可以填1,2,3
。
答案:
解析:本题主要考查除数是两位数的除法的试商方法。
首先我们要知道三位数除以两位数时,如何判断商是几位数。
当被除数的前两位大于或等于除数时,商是两位数;
当被除数的前两位小于除数时,商是一位数。
现在,给定的被除数是□51,除数是45。
要使商是两位数,那么被除数的前两位,也就是□5,必须大于或等于45。
考虑到□是一个数字,它可以是1到9之间的任何数字。
那么,满足□5大于或等于45的数字有:4,5,6,7,8,9。
所以,要使商是两位数,□里可以填4,5,6,7,8,9中的任意一个。
接下来,要使商是一位数,被除数的前两位□5必须小于45。
满足这个条件的数字有:1,2,3。
(因为0不能作为整数的最高位,所以不考虑0)
所以,要使商是一位数,□里可以填1,2,3中的任意一个。
答案:4,5,6,7,8,9;1,2,3。
首先我们要知道三位数除以两位数时,如何判断商是几位数。
当被除数的前两位大于或等于除数时,商是两位数;
当被除数的前两位小于除数时,商是一位数。
现在,给定的被除数是□51,除数是45。
要使商是两位数,那么被除数的前两位,也就是□5,必须大于或等于45。
考虑到□是一个数字,它可以是1到9之间的任何数字。
那么,满足□5大于或等于45的数字有:4,5,6,7,8,9。
所以,要使商是两位数,□里可以填4,5,6,7,8,9中的任意一个。
接下来,要使商是一位数,被除数的前两位□5必须小于45。
满足这个条件的数字有:1,2,3。
(因为0不能作为整数的最高位,所以不考虑0)
所以,要使商是一位数,□里可以填1,2,3中的任意一个。
答案:4,5,6,7,8,9;1,2,3。
6. 在○里填上“>”“<”或“=”。
62÷20
62÷20
>
60÷20 900÷36>
900÷40 36÷24=
(36÷2)÷(24÷2)
答案:
解析:本题考查除法运算以及数值的大小比较。对于每一组表达式,我们需要先计算出每个表达式的值,然后进行比较。
答案:
(1) 对于 62÷20 和 60÷20:
62÷20 = 3.1
60÷20 = 3
因为 3.1 > 3,所以 62÷20 > 60÷20。
(2) 对于 900÷36 和 900÷40:
900÷36 = 25
900÷40 = 22.5
因为 25 > 22.5,所以 900÷36 > 900÷40。
(3) 对于 36÷24 和 (36÷2)÷(24÷2):
36÷24 = 1.5
(36÷2)÷(24÷2) = 18÷12 = 1.5
两者相等,所以 36÷24 = (36÷2)÷(24÷2)。
综上,答案为:>,>,=。
答案:
(1) 对于 62÷20 和 60÷20:
62÷20 = 3.1
60÷20 = 3
因为 3.1 > 3,所以 62÷20 > 60÷20。
(2) 对于 900÷36 和 900÷40:
900÷36 = 25
900÷40 = 22.5
因为 25 > 22.5,所以 900÷36 > 900÷40。
(3) 对于 36÷24 和 (36÷2)÷(24÷2):
36÷24 = 1.5
(36÷2)÷(24÷2) = 18÷12 = 1.5
两者相等,所以 36÷24 = (36÷2)÷(24÷2)。
综上,答案为:>,>,=。
7. 花店有615枝花,如果每次用28枝花制作花篮,能做(
21
)个花篮,还余(27
)枝花。
答案:
解析:本题考查的是利用除法解决实际问题,涉及到有余数的除法。
首先,我们用总的花的数量除以每个花篮需要的花的数量,即:
$615 ÷ 28 = 21$(个)$\ldots\ldots 27$(枝)
所以能做21个花篮,还余27枝花。
答案:21;27。
首先,我们用总的花的数量除以每个花篮需要的花的数量,即:
$615 ÷ 28 = 21$(个)$\ldots\ldots 27$(枝)
所以能做21个花篮,还余27枝花。
答案:21;27。
8. 一个三位数除以一个两位数,商最多是(
两
)位数,最少是(一
)位数。
答案:
解析:
本题考查除法运算中商位数的判断。
对于一个三位数除以一个两位数,我们首先要理解除法的基本原理。
当被除数最大(接近但小于999),除数最小时(接近但大于10),商会是最大的。例如,999除以11,商是90余9,是一个两位数,但接近三位数的边缘情况我们不考虑它真正达到三位数,因为只有当除数是个位数时,商才可能达到三位数,但题目限定除数是两位数。所以,在常规情况下,我们考虑最大的商是两位数中的较大值。
当被除数最小(100),除数最大(99)时,商会是最小的。100除以99,商是1余1,商是一位数。
所以,一个三位数除以一个两位数,商最多是两位数,最少是一位数。
答案:
两;一。
本题考查除法运算中商位数的判断。
对于一个三位数除以一个两位数,我们首先要理解除法的基本原理。
当被除数最大(接近但小于999),除数最小时(接近但大于10),商会是最大的。例如,999除以11,商是90余9,是一个两位数,但接近三位数的边缘情况我们不考虑它真正达到三位数,因为只有当除数是个位数时,商才可能达到三位数,但题目限定除数是两位数。所以,在常规情况下,我们考虑最大的商是两位数中的较大值。
当被除数最小(100),除数最大(99)时,商会是最小的。100除以99,商是1余1,商是一位数。
所以,一个三位数除以一个两位数,商最多是两位数,最少是一位数。
答案:
两;一。
二、判断并说理
1. 三位数除以两位数,商一定是两位数。 ………………………(
我的想法:
2. 1420÷70=20……2。 ……………………………………(
20
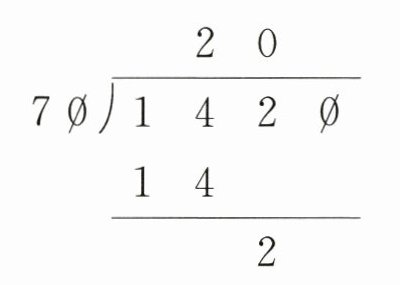
70)1420
14
---
2
我的想法:
1. 三位数除以两位数,商一定是两位数。 ………………………(
×
)我的想法:
三位数除以两位数,商可能是一位数,也可能是两位数。例如$100÷50 = 2$,商是一位数;$990÷11=90$,商是两位数。所以“三位数除以两位数,商一定是两位数”这种说法是错误的。
2. 1420÷70=20……2。 ……………………………………(
×
)20
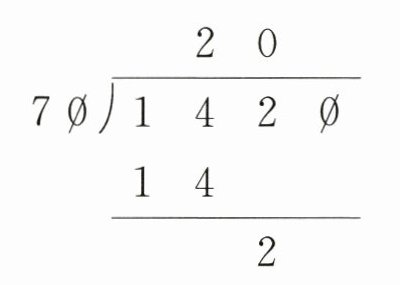
70)1420
14
---
2
我的想法:
根据有余数的除法,$被除数 = 商×除数 + 余数$。在$1420÷70$中,$70×20 + 2=1400 + 2 = 1402\neq1420$。
正确的计算是$1420÷70 = 20\cdots\cdots20$,因为$70×20+20 = 1400 + 20=1420$,所以原计算错误。
正确的计算是$1420÷70 = 20\cdots\cdots20$,因为$70×20+20 = 1400 + 20=1420$,所以原计算错误。
答案:
1. ×
想法:三位数除以两位数,商可能是一位数,也可能是两位数。例如$100÷50 = 2$,商是一位数;$990÷11=90$,商是两位数。所以“三位数除以两位数,商一定是两位数”这种说法是错误的。
2. ×
想法:根据有余数的除法,$被除数 = 商×除数 + 余数$。在$1420÷70$中,$70×20 + 2=1400 + 2 = 1402\neq1420$。
正确的计算是$1420÷70 = 20\cdots\cdots20$,因为$70×20+20 = 1400 + 20=1420$,所以原计算错误。
想法:三位数除以两位数,商可能是一位数,也可能是两位数。例如$100÷50 = 2$,商是一位数;$990÷11=90$,商是两位数。所以“三位数除以两位数,商一定是两位数”这种说法是错误的。
2. ×
想法:根据有余数的除法,$被除数 = 商×除数 + 余数$。在$1420÷70$中,$70×20 + 2=1400 + 2 = 1402\neq1420$。
正确的计算是$1420÷70 = 20\cdots\cdots20$,因为$70×20+20 = 1400 + 20=1420$,所以原计算错误。
查看更多完整答案,请扫码查看


